题目内容
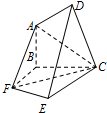 (2012•安徽模拟)如图,在五面体中,平面ABCD⊥平面BFEC,Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,AB=AD=FB=FE=1,斜边AC=FC=2.
(2012•安徽模拟)如图,在五面体中,平面ABCD⊥平面BFEC,Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,AB=AD=FB=FE=1,斜边AC=FC=2.(Ⅰ)证明:AF∥DE;
(Ⅱ)求棱锥D-BCEF的体积.
分析:(1)由题设知AB⊥BC,FB⊥BC,sin∠ACB=
,故∠ACB=30°,∠DCB=60°,作DM⊥BC于M点,连接EM,证明△DMC≌△EMC,由此能够推导出AF∥DE.
(2)由平面ABCD⊥平面BFEC,DM⊥BC,知DM⊥平面BCEF,由DC=BC=
=
,知DM=DC•sin∠DCM=
•
=
,由此能求出棱锥D-BCEF的体积.
| 1 |
| 2 |
(2)由平面ABCD⊥平面BFEC,DM⊥BC,知DM⊥平面BCEF,由DC=BC=
| 4-1 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
解答: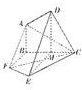 解:(1)∵在五面体中,平面ABCD⊥平面BFEC,
解:(1)∵在五面体中,平面ABCD⊥平面BFEC,
Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,
AB=AD=FB=FE=1,斜边AC=FC=2,
∴AB⊥BC,FB⊥BC,sin∠ACB=
,
∴∠ACB=30°,∠DCB=60°,
如图,作DM⊥BC于M点,连接EM,
在△DMC和△EMC中,∠MCD=∠MCE=60°,
CD=CE,CM=CM,
∴△DMC≌△EMC,∴∠DMC=∠EMC=90°,
故EM⊥BC,
∴EM∥BF,DM∥AB,∴面DEM∥面ABF,
面ADEF∩面ABF=AF,
面ADEF∩面DEM=DE,
∴AF∥DE.
(2)∵平面ABCD⊥平面BFEC,DM⊥BC,
∴DM⊥平面BCEF,
∵DC=BC=
=
,
∴DM=DC•sin∠DCM=
•
=
,
∴S四边形BCEF=2S△ABC=2×
×BC×AB=2×
×1×
=
,
∴棱锥D-BCEF的体积V=
×
×
=
.
 解:(1)∵在五面体中,平面ABCD⊥平面BFEC,
解:(1)∵在五面体中,平面ABCD⊥平面BFEC,Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,
AB=AD=FB=FE=1,斜边AC=FC=2,
∴AB⊥BC,FB⊥BC,sin∠ACB=
| 1 |
| 2 |
∴∠ACB=30°,∠DCB=60°,
如图,作DM⊥BC于M点,连接EM,
在△DMC和△EMC中,∠MCD=∠MCE=60°,
CD=CE,CM=CM,
∴△DMC≌△EMC,∴∠DMC=∠EMC=90°,
故EM⊥BC,
∴EM∥BF,DM∥AB,∴面DEM∥面ABF,
面ADEF∩面ABF=AF,
面ADEF∩面DEM=DE,
∴AF∥DE.
(2)∵平面ABCD⊥平面BFEC,DM⊥BC,
∴DM⊥平面BCEF,
∵DC=BC=
| 4-1 |
| 3 |
∴DM=DC•sin∠DCM=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴S四边形BCEF=2S△ABC=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴棱锥D-BCEF的体积V=
| 1 |
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查直线平行的证明,考查棱锥的体积的计算,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目