题目内容
(本题满分9分)在平面直角坐标系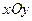 中,已知直线
中,已知直线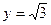 被圆
被圆
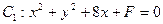 截得的弦长为
截得的弦长为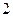 .
.
(1)求圆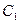 的方程;
的方程;
(2)设圆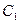 和
和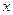 轴相交于
轴相交于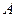 ,
,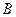 两点,点
两点,点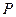 为圆
为圆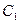 上不同于
上不同于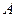 ,
,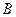 的任意一点,直线
的任意一点,直线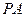 ,
,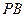 交
交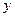 轴于
轴于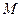 ,
,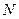 两点.当点
两点.当点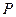 变化时,以
变化时,以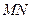 为直径的圆
为直径的圆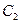 是否经过圆
是否经过圆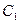 内一定点?请证明你的结论;
内一定点?请证明你的结论;
(3)若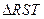 的顶点
的顶点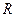 在直线
在直线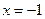 上,
上,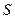 ,
,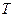 在圆
在圆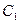 上,且直线
上,且直线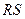 过圆心
过圆心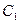 ,
,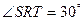 ,求点
,求点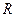 的纵坐标的范围.
的纵坐标的范围.
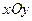 中,已知直线
中,已知直线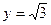 被圆
被圆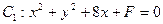 截得的弦长为
截得的弦长为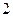 .
.(1)求圆
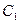 的方程;
的方程;(2)设圆
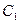 和
和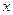 轴相交于
轴相交于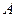 ,
,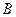 两点,点
两点,点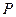 为圆
为圆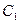 上不同于
上不同于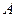 ,
,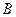 的任意一点,直线
的任意一点,直线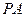 ,
,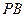 交
交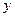 轴于
轴于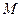 ,
,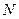 两点.当点
两点.当点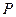 变化时,以
变化时,以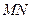 为直径的圆
为直径的圆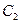 是否经过圆
是否经过圆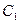 内一定点?请证明你的结论;
内一定点?请证明你的结论;(3)若
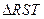 的顶点
的顶点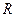 在直线
在直线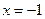 上,
上,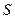 ,
,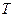 在圆
在圆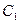 上,且直线
上,且直线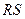 过圆心
过圆心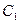 ,
,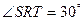 ,求点
,求点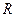 的纵坐标的范围.
的纵坐标的范围.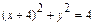 ,
,当点P变化时,以MN为直径的圆
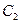 经过圆
经过圆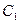 内一定点
内一定点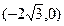 .
.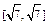
25.解:(1)圆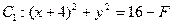 ,
,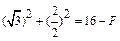 ,
,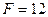 ,
,
 圆
圆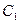 的方程为
的方程为 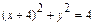 . (3分)
. (3分)
(2)设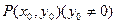 ,则
,则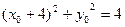

 ,则
,则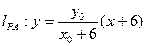 ,得
,得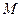
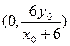 (4分)
(4分)

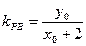 ,则
,则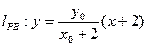 , 得
, 得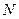
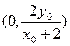 (5分)
(5分)
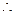 圆
圆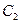 的方程并化简为
的方程并化简为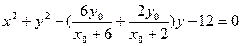 (5分)
(5分)
令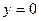 ,得
,得 ,又点
,又点 在圆
在圆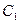 内
内
所以当点P变化时,以MN为直径的圆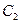 经过圆
经过圆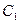 内一定点
内一定点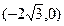 . (7分)
. (7分)
(3)设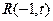 ,作
,作 于
于 ,设
,设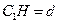 ,由于
,由于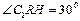 ,
,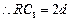 ,由题得
,由题得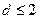 ,
,  ,即
,即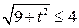 ,
,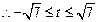 ,点
,点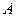 的纵坐标的范围为
的纵坐标的范围为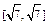 . (9分)
. (9分)
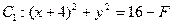 ,
,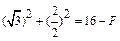 ,
,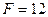 ,
, 圆
圆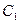 的方程为
的方程为 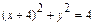 . (3分)
. (3分)(2)设
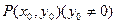 ,则
,则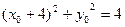

 ,则
,则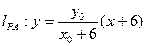 ,得
,得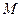
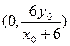 (4分)
(4分) 
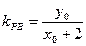 ,则
,则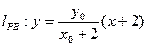 , 得
, 得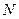
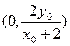 (5分)
(5分) 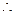 圆
圆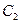 的方程并化简为
的方程并化简为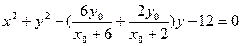 (5分)
(5分)令
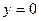 ,得
,得 ,又点
,又点 在圆
在圆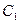 内
内所以当点P变化时,以MN为直径的圆
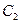 经过圆
经过圆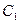 内一定点
内一定点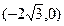 . (7分)
. (7分)(3)设
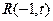 ,作
,作 于
于 ,设
,设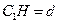 ,由于
,由于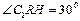 ,
,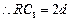 ,由题得
,由题得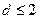 ,
,  ,即
,即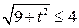 ,
,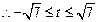 ,点
,点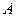 的纵坐标的范围为
的纵坐标的范围为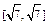 . (9分)
. (9分)
练习册系列答案
相关题目
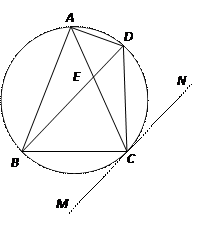
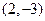 关于直线
关于直线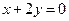 的对称点仍在这个圆上,且圆与
的对称点仍在这个圆上,且圆与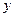 轴相切,求圆的方程。
轴相切,求圆的方程。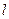 通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线
通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线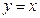 上。
上。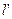 的方程;
的方程;
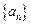 满足:
满足: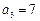 ,
,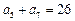 .
.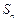 .
.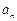 及
及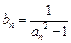 (
(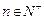 ),求数列
),求数列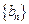 的前n项和
的前n项和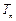 .
.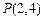 向圆
向圆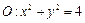 作切线,求切线的方程;
作切线,求切线的方程;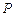 在圆
在圆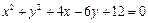 上,点
上,点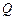 在直线
在直线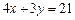 上,求
上,求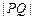 的最小值.
的最小值. 与圆
与圆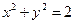 相切,则
相切,则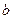 的值为
的值为


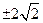
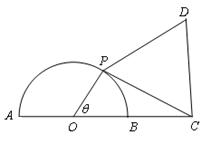
 的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D
的半径为1,点C在直径AB的延长线上,BC=1,点P是半圆上的一个动点,以PC为边作正三角形PCD,且点D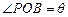 ,试将四边形OPDC的面积
,试将四边形OPDC的面积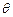 的函数
的函数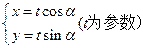 与圆
与圆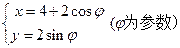 相切,则直线的倾斜角
相切,则直线的倾斜角 为( )
为( )