题目内容
12．已知|a-b|=|a|+|b|，且|a|=5，|b|=3，求ab的值．分析 由题意可得a=5、b=-3，或a=-5、b=3，由此可得ab的值．
解答 解：由|a-b|=|a|+|b|，且|a|=5，|b|=3，可得a=5、b=-3，或a=-5、b=3，
∴ab=5-3=$\frac{1}{125}$，或 ab=（-5）3=-125．
点评 本题主要考查绝对值的意义，属于基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2．下列函数中指数函数的个数为（ ）
①y=（$\frac{1}{2}$）x-1；②y=2•3x；③y=ax（a＞0且a≠1）；④y=1x；⑤y=（$\frac{1}{2}$）2x-1．
①y=（$\frac{1}{2}$）x-1；②y=2•3x；③y=ax（a＞0且a≠1）；④y=1x；⑤y=（$\frac{1}{2}$）2x-1．
| A． | 1个 | B． | 2个 | C． | 4个 | D． | 5个 |
17．边长与对角线长均相等的空间四边形ABCD中，AB与CD的中点分别是P、Q，作与直线PQ垂直的任一平面α，则空间四边形ABCD在平面α内的射影是（ ）
| A． | 梯形 | B． | 矩形但非正方形 | C． | 菱形但非正方形 | D． | 正方形 |
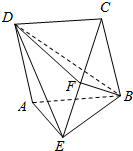如图，已知矩形ABCD，BC⊥平面ABE，F为CE的中点．