题目内容
4.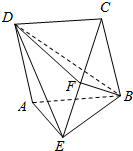 如图,已知矩形ABCD,BC⊥平面ABE,F为CE的中点.
如图,已知矩形ABCD,BC⊥平面ABE,F为CE的中点.(1)求证:直线AE∥平面BDF;
(2)若AE=BE=$\frac{\sqrt{2}}{2}$AB,求证:AE⊥平面BCE.
分析 (1)设AC∩BD=G,连结FG,易知G是AC的中点,可证FG∥AE,从而可证AE∥平面BDF.
(2)由已知可得AE2+BE2=AB2,由勾股定理可得AE⊥BE,又BC⊥平面ABE,可得:BC⊥AE,BE∩∩BE=B,即可证明AE⊥平面BCE.
解答  证明:(1)设AC∩BD=G,连结FG,易知G是AC的中点,
证明:(1)设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE.…(2分)
因为 AE?平面BDF,FG?平面BDF,
所以 AE∥平面BDF. …(6分)
(2)因为AE=BE=$\frac{\sqrt{2}}{2}$AB,
所以AE2+BE2=AB2,可得:AE⊥BE,
又因为BC⊥平面ABE,可得:BC⊥AE,又BE∩BE=B,
∴AE⊥平面BCE.
点评 本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,连接GF,证明FG∥AE是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.由y=$\frac{1}{x}$-2,y=0,x=2所对应的曲线围成的封闭图形的面积为( )
| A. | ln2-1 | B. | 1-ln2 | C. | 2ln2-3 | D. | 3-2ln2 |
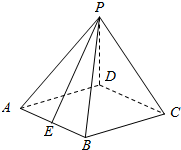 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.