题目内容
若关于x的不等式x2-(a-1)x>-4对于x∈R恒成立,则a的取值范围是______.
∵x2-(a-1)x>-4对于x∈R恒成立,
∴x2-(a-1)x+4>0对于x∈R恒成立,
令f(x)=x2-(a-1)x+4,
则f(x)=x2-(a-1)x+4的图象恒在x轴上方,
∴[-(a-1)]2-4×4<0,
即a2-2a-15<0,
解得:-3<a<5.
∴a的取值范围是(-3,5).
故答案为:(-3,5).
∴x2-(a-1)x+4>0对于x∈R恒成立,
令f(x)=x2-(a-1)x+4,
则f(x)=x2-(a-1)x+4的图象恒在x轴上方,
∴[-(a-1)]2-4×4<0,
即a2-2a-15<0,
解得:-3<a<5.
∴a的取值范围是(-3,5).
故答案为:(-3,5).

练习册系列答案
相关题目

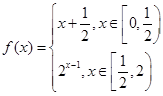 ,若存在
,若存在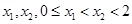 时,
时,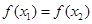 ,则
,则 的取值范围是________________。
的取值范围是________________。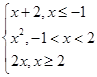 ,若f(x)=3,则x的值是 .
,若f(x)=3,则x的值是 .