题目内容
已知函数f(x)=x3-ax,g(x)=
x2-lnx-
(1)若对一切x∈(0,+∞),有不等式f(x)≥2x•g(x)-x2+5x-3恒成立,求实数a的取值范围;
(2)记G(x)=
x2-
-g(x),求证:G(x)>
-
.
| 1 |
| 2 |
| 5 |
| 2 |
(1)若对一切x∈(0,+∞),有不等式f(x)≥2x•g(x)-x2+5x-3恒成立,求实数a的取值范围;
(2)记G(x)=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| ex |
| 2 |
| ex |
(1)原不等式可化为:x3-ax≥2x(
x2-lnx-
)-x2+5x-3,化简得:ax≤2xlnx+x2+3,
∵x>0,故上式可化为a≤2lnx+
+x恒成立,则问题等价于a≤(2lnx+
+x)min.
记t(x)=2lnx+
+x,(x>0),t′(x)=
,
令t′(x)=0,得x=1,
∵x>0,∴在(0,1)上,t′(x)<0,在(1,+∞)上,t′(x)>0,
∴t(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故当x=1时,t(x)有最小值为4,故a≤4,
∴实数a的取值范围是a∈(-∞,4];
(2)化简得,G(x)=lnx,则原不等式可化为lnx>
-
,即证xlnx>
-
成立,
记F(x)=xlnx,则F'(x)=lnx+1,
当0<x<
时,F'(x)<0,F(x)递减;当x>
时,F'(x)>0,F(x)递增,
故当x=
时,F(x)取得极小值,也为最小值,其最小值为F(
)=-
.
记H(x)=
-
,则H'(x)=
,
当0<x<1时,H'(x)>0,H(x)递增;当x>1时,H'(x)<0,H(x)递减;
故当x=1时,H(x)取得极大值,也为最大值,其最大值为H(1)=-
,
由函数F(x)的最小值与函数H(x)的最大值不能同时取到,
故x∈(0,+∞)时,F(x)>H(x),故原不等式成立.
| 1 |
| 2 |
| 5 |
| 2 |
∵x>0,故上式可化为a≤2lnx+
| 3 |
| x |
| 3 |
| x |
记t(x)=2lnx+
| 3 |
| x |
| x2+2x-3 |
| x2 |
令t′(x)=0,得x=1,
∵x>0,∴在(0,1)上,t′(x)<0,在(1,+∞)上,t′(x)>0,
∴t(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
故当x=1时,t(x)有最小值为4,故a≤4,
∴实数a的取值范围是a∈(-∞,4];
(2)化简得,G(x)=lnx,则原不等式可化为lnx>
| 1 |
| ex |
| 2 |
| ex |
| x |
| ex |
| 2 |
| e |
记F(x)=xlnx,则F'(x)=lnx+1,
当0<x<
| 1 |
| e |
| 1 |
| e |
故当x=
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
记H(x)=
| x |
| ex |
| 2 |
| e |
| 1-x |
| ex |
当0<x<1时,H'(x)>0,H(x)递增;当x>1时,H'(x)<0,H(x)递减;
故当x=1时,H(x)取得极大值,也为最大值,其最大值为H(1)=-
| 1 |
| e |
由函数F(x)的最小值与函数H(x)的最大值不能同时取到,
故x∈(0,+∞)时,F(x)>H(x),故原不等式成立.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
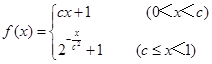 ,且
,且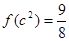 .
.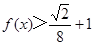 .
.

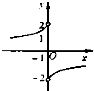

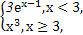 则f(f(1))的值等于 .
则f(f(1))的值等于 .