题目内容
某学校共有高一、高二、高三学生2000名,各年级男、女生人数如图: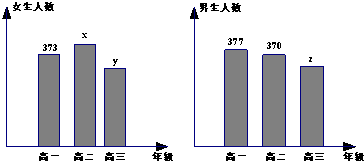
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知y≥245,z≥245,求高三年级中女生比男生多的概率.

已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知y≥245,z≥245,求高三年级中女生比男生多的概率.
分析:(1)根据题意,有全校共有学生2000名,其中高二年级女生x名,且抽到高二年级女生的概率是0.19,结合频率、频数和样本容量之间的关系,可得
=0.19,解可得答案;
(2)根据高二男女生一起750人,又高一学生750人,所以高三男女生一起500人,按分层抽样,做出高三年级应抽取的人数;
(3)根据所给的条件列举出所有的情况,可得其情况数目,同时可得女生比男生多的情况数目,由等可能事件的概率公式,计算可得答案.
| x |
| 2000 |
(2)根据高二男女生一起750人,又高一学生750人,所以高三男女生一起500人,按分层抽样,做出高三年级应抽取的人数;
(3)根据所给的条件列举出所有的情况,可得其情况数目,同时可得女生比男生多的情况数目,由等可能事件的概率公式,计算可得答案.
解答:解:(1)根据题意,全校共有学生2000名,其中高二年级女生x名,
且抽到高二年级女生的概率是0.19,则有
=0.19,
∴x=380;
(2)由图可得,高二男生有370人,则高二男女生一起750人,高一学生750人,
所以高三男女生共2000-750-750=500人,
按分层抽样,高三年级应抽取
×500=12人;
(3)因为y+z=500,y≥245,z≥245,所以基本事件有:
y=245,z=255;y=246,z=254;y=247,z=253;y=248,z=252;y=249,z=251;y=250,z=250;
y=251,z=249;y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245;一共11个基本事件.
其中女生比男生多,即y>z的基本事件有:
y=251,z=249,y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245
共5个基本事件,
故女生必男生多的事件的概率为
且抽到高二年级女生的概率是0.19,则有
| x |
| 2000 |
∴x=380;
(2)由图可得,高二男生有370人,则高二男女生一起750人,高一学生750人,
所以高三男女生共2000-750-750=500人,
按分层抽样,高三年级应抽取
| 48 |
| 2000 |
(3)因为y+z=500,y≥245,z≥245,所以基本事件有:
y=245,z=255;y=246,z=254;y=247,z=253;y=248,z=252;y=249,z=251;y=250,z=250;
y=251,z=249;y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245;一共11个基本事件.
其中女生比男生多,即y>z的基本事件有:
y=251,z=249,y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245
共5个基本事件,
故女生必男生多的事件的概率为
| 5 |
| 11 |
点评:本题考查古典概型计算与频率直方图的使用,关键是正确使用频率分步直方图,其次是在列举所有的事件时,做到不重不漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
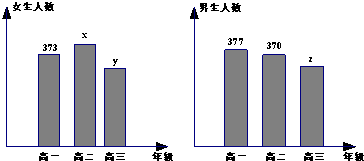 某学校共有高一、高二、高三学生2000名,各年级男、女生人数如图:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
某学校共有高一、高二、高三学生2000名,各年级男、女生人数如图:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
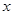 的值;
的值;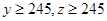 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率. 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图: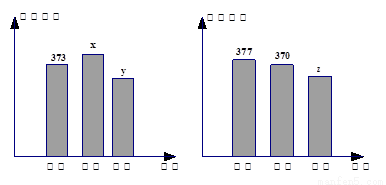
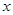 的值;
的值;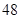 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?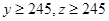 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率. 名,各年级男、女生人数如下图:
名,各年级男、女生人数如下图: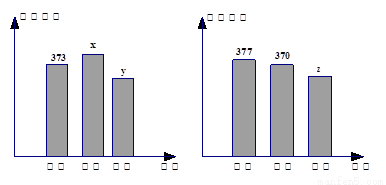
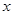 的值;
的值;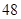 名学生,问应在高三年级抽取多少名?
名学生,问应在高三年级抽取多少名?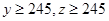 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.