题目内容
已知过抛物线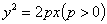 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于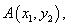
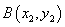 (
(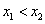 )两点,且
)两点,且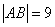 .
.
(1)求该抛物线的方程;
(2)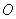 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若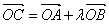 ,求
,求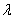 的值.
的值.
【答案】
(1)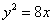 (2)
(2)
【解析】
试题分析:解析:(1)直线AB的方程是
所以: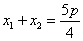 ,由抛物线定义得:
,由抛物线定义得: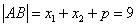 ,所以p=4,
,所以p=4,
抛物线方程为: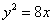
(2)、由p=4,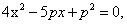 化简得
化简得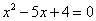 ,从而
,从而
 ,从而A:(1,
,从而A:(1, ),B(4,
),B(4,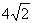 )
)
设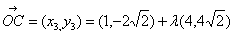 =
=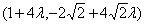 ,又
,又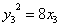 ,即
,即 8(4
8(4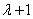 ),即
),即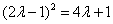 ,解得
,解得
考点:抛物线的方程,直线与抛物线的位置关系
点评:解决的关键是根据联立方程组结合已知中的抛物线的性质来得到求解,属于检测。同事能结合根与系数的关系得到交点坐标,进而求解参数的值,属于基础题。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 已知过抛物线
已知过抛物线 的焦点
的焦点 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于 两点,且
两点,且 ,则
,则 .
. 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
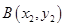 (
( )两点,且
)两点,且 .
. 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值. 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于 ,
,
 两点,且
两点,且 .
. 为坐标原点,是否存在平行于
为坐标原点,是否存在平行于 的直线
的直线 ,使得直线
,使得直线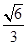 ?若存在,求出直线
?若存在,求出直线 的焦点
的焦点 的直线交该抛物线于
的直线交该抛物线于 、
、 两点,
两点, ,则
,则 _ _
.
_ _
.