Question

某种股票的价格y（元）在一年内与月份x（月）之间的函数关系如下表：

x	0	1	2	3	4	5	6
y	10.1	10.2	10.4	10.8	11.6	13.2	16.4

（Ⅰ）在直角坐标系中，通过描点、连线，猜测并确定y与x之间的函数关系式；
（Ⅱ）预测这种股票在8月份时的价格，以及价格为112.4元时的月份．

Answer 1

（Ⅰ）函数图象如图所示，

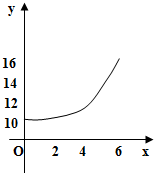
猜测一：y是x的二次函数模型，
设y与x之间的函数关系式为y=ax²+bx+c，
将（0，10.1）、（1，10.2）、（2，10.4）代入，
得

c=10.1 a+b+c=10.2 4a+2b+c=10.4

，
∴a=b=0.05，c=10.1．
∴y=f（x）=0.05x²+0.05x+10.1．
f（3）=10.7，f（4）=11.1，f（5）=11.6，f（6）=12.2均不合题意．
猜测二：y是x的指数函数模型，设y与x之间的函数关系式为y=b•a^x+c，
将（0，10.1）、（1，10.2）、（2，10.4）代入，
得

b+c=10.1 ab+c=10.2 a2b+c=10.4

⇒

ab-b=0.1 a2b-ab=0.2

，⇒

(a-1)b=0.1 (a-1)ab=0.2

，
∴a=2，b=0.1．从而c=10．
∴y=f(x)=

1

10

•2x+10．
f（3）=10.8，f（4）=11.6，f（5）=13.2，f（6）=16.4均符合题意．
故y与x之间的函数关系式为∴y=f(x)=

1

10

•2x+10．
（Ⅱ）f(8)=

1

10

•28+10=35.6，112.4=

1

10

•2x+10，
解得x=10．
所以这种股票在8月份时的价格约为35.6元，价格为112.4元时的月份是10月份．