题目内容
【题目】已知椭圆C：
的离心率为
，与坐标轴分别交于A，B两点，且经过点Q（
，1）．
（Ⅰ）求椭圆C的标准方程；
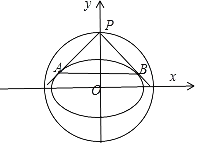
（Ⅱ）若P（m，n）为椭圆C外一动点，过点P作椭圆C的两条互相垂直的切线l1、l2，求动点P的轨迹方程，并求△ABP面积的最大值．
【答案】（Ⅰ）
1；（Ⅱ）
．
【解析】
（Ⅰ）由离心率及椭圆过的点的坐标，及a，b，c之间的关系可得a，b的值，进而求出椭圆的方程；
（Ⅱ）过P的两条切线分斜率存在和不存在两种情况讨论，当斜率不存在时，直接由椭圆的方程可得切点A，B的坐标，当切线的斜率存在且不为0时，设过P的切线方程，与椭圆联立．由判别式等于0可得参数的关系，进而可得PA，PB的斜率之积，进而可得m，n之间的关系，即P的轨迹方程，显然切线斜率不存在时的点P也在轨迹方程上；因为PA，PB互相垂直，所以三角形PAB的面积为S△ABP
|PA||PB|
，当且仅当|PA|＝|PB|时取等号，此时得到点P的坐标求解.
（Ⅰ）由题意可得e
，
1，c2＝a2﹣b2，解得a2＝4，b2＝2，
所以椭圆的方程为：
1；
（Ⅱ）设两个切点分别为A，B，①当两条切线中有一条斜率不存在时，
即A，B两点分别位于椭圆的长轴和短轴的端点，此时P的坐标为：（±2，±
），
②当两条切线的斜率存在且不为0时，设过P的切线的方程为：y﹣n＝k（x﹣m），
联立直线y﹣n＝k（x﹣m）和椭圆的方程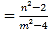
，整理可得（1+2k2）x2﹣4k（km﹣n）x+2（km﹣n）2﹣4＝0，
由题意可得△＝16k2（km﹣n）2﹣4（1+2k2）[2（km﹣n）2﹣4]＝0，整理可得（m2﹣4）k2﹣2kmn+n2﹣2＝0，所以k1k2
，
设直线PA，PB的斜率分别为k1，k2，则k1k2，
而PA，PB互相垂直，所以
1，
即m2+n2＝6，（m≠±2），
又因为P（±2，
）在m2+n2＝6上，
所以点P在圆x2+y2＝6上．
因为l1⊥l2，
所以span>S△ABP|PA||PB|，当且仅当|PA|＝|PB|时取等号，
即P在椭圆的短轴所在的直线上时即P（0，
），
由圆及椭圆的对称性设P（0，
），则直线PA的斜率为1，可得直线PA的方程为：y＝x
，
代入椭圆的方程可得3x2+4x+8＝0，解得x
，y
，即A（
，
），
所以|PA|
，所以AB2＝2|PA|2
，
所以（S△ABP）max
．
