题目内容
20.设f(x)=sinπx3,则:f(1)+f(2)+f(3)+…+f(2012)=√3.分析 由三角函数的周期公式求很粗f(x)的周期,并求出一个周期内的所有函数值,利用周期性求出式子的值.
解答 解:由题意得,函数f(x)的周期T=2ππ3=6,
∴f(1)=sinπ3=√32,f(2)=sin2π3=√32,f(3)=sinπ=0,f(4)=sin4π3=-√32,
f(5)=sin5π3=-√32,f(6)=sin2π=0,
∴f(1)+f(2)+f(3)+…+f(6)=0,
∵2012=335×6+2,
∴f(1)+f(2)+f(3)+…+f(2012)=f(1)+f(2)=√32+√32=√3,
故答案为:√3.
点评 本题考查利用函数的周期性求函数值,以及三角函数的周期公式,属于基础题.

练习册系列答案
相关题目
11.如图所示的程序框图中,若x=5,则输出i的值是( )
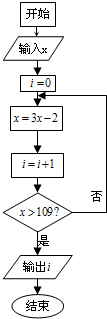

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.在△ABC中,c=√2,acosC=csinA,若当a=x0时的△ABC有两解,则x0的取值范围是( )
| A. | (1,√2) | B. | (1,√3) | C. | (√3,2) | D. | (√2,2) |
15.在△ABC中,若c2+ab=a2+b2,则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
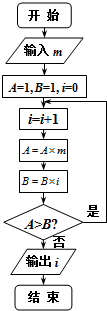

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.已知双曲线x2a2-y2b2=1(a>0,b>0),两个焦点分别为F1、F2,若在第一象限内双曲线上存在一点P,使得在△PF1F2中,∠PF1F2=30°,∠PF2F1=90°,则此双曲线的渐近线方程为( )
| A. | y=±√22x | B. | y=±√2x | C. | y=±√3x | D. | y=±2x |
