题目内容
经市场调查,某商品在30天内,其销售量(单位:件)和价格(单位:元)均为时间t(单位:天)的函数,且销售量近似地满足关系g(t)=-t+100(t∈N,0<t≤30),在前15天里价格为f(t)=t+80(t∈N,0<t≤15),在后15天里价格为f(t)=-
t+101(t∈N,16≤t≤30).
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求这种商品的日销售额的最大值.
| 1 |
| 16 |
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求这种商品的日销售额的最大值.
(1)当0<t≤15时,S=g(t)f(t)=(-t+100)(t+80);
当16≤t≤30时,S=g(t)f(t)=(-t+100)(-
t+101),
所以该种商品的日销售额S与时间t的函数关系为:S=
;
(2)当0<t≤15时,S=(-t+100)(t+80)=-(t-10)2+8100.
当t=10时,Smax=8100.
当16≤t≤30时,S=(-t+100)(-
+101)=
t2-
t+10100,
易知此时S在[16,30]上递减,所以当t=16时,Smax=8400.
日销售额的最大值为8400元.
综上可得,当t=16时,日销售额的最大值为8400元.
当16≤t≤30时,S=g(t)f(t)=(-t+100)(-
| 1 |
| 16 |
所以该种商品的日销售额S与时间t的函数关系为:S=
|
(2)当0<t≤15时,S=(-t+100)(t+80)=-(t-10)2+8100.
当t=10时,Smax=8100.
当16≤t≤30时,S=(-t+100)(-
| t |
| 16 |
| 1 |
| 16 |
| 429 |
| 4 |
易知此时S在[16,30]上递减,所以当t=16时,Smax=8400.
日销售额的最大值为8400元.
综上可得,当t=16时,日销售额的最大值为8400元.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
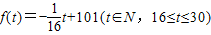 .
.