题目内容
经市场调查,某商品在过去100天内的销售量和销售价格均为时间t(天)的函数,且日销售量近似的满足g(t)=-
t+
(1≤t≤100,t∈N*),前40天价格为f(t)=
t+22(1≤t≤40,t∈N*),后60天价格为f(t)=
t+52(41≤t≤100,t∈N*).试求该商品的日销售额S(t)的最大值和最小值.
| 1 |
| 3 |
| 112 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
分析:根据题意,可对t分1≤t≤40,t∈N*时,与41≤t≤100,t∈N*时两种情况下可分别求得S(t)=g(t)f(t)的表达式,利用二次函数的对称轴与所给区间之间的关系利用函数的单调性
即可求得该商品的日销售额S(t)的最大值和最小值.
即可求得该商品的日销售额S(t)的最大值和最小值.
解答:解:当1≤t≤40,t∈N*时,
S(t)=g(t)f(t)
=(-
t+
)(
t+22)
=-
(t-12)2+
,
∴768=S(40)≤S(t)≤S(12)=
+12=
…6分
当41≤t≤100,t∈N*时,
S(t)=g(t)f(t)
=(-
t+
)(-
t+52)
=
(t-108)2-
,
∴8=S(100)≤S(t)≤S(41)=
…12分
∴S(t)的最大值为
,最小值为8…14分.
S(t)=g(t)f(t)
=(-
| 1 |
| 3 |
| 112 |
| 3 |
| 1 |
| 4 |
=-
| 1 |
| 12 |
| 2500 |
| 3 |
∴768=S(40)≤S(t)≤S(12)=
| 112×22 |
| 3 |
| 2500 |
| 3 |
当41≤t≤100,t∈N*时,
S(t)=g(t)f(t)
=(-
| 1 |
| 3 |
| 112 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
| 8 |
| 3 |
∴8=S(100)≤S(t)≤S(41)=
| 1491 |
| 2 |
∴S(t)的最大值为
| 2500 |
| 3 |
点评:本题考查函数的最值,突出考查二次函数的单调性,根据二次函数的对称轴与所给区间之间的关系判断函数的单调性是关键,也是难点,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
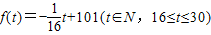 .
.