题目内容
14．数列{an}共有六项，其中四项是1，其余两项各不相同，则满足上述条件的数列{an}共有（ ）| A． | 30个 | B． | 31个 | C． | 60个 | D． | 61个 |
分析 先排各不相同的两项，有${A}_{6}^{2}$种排法，其余4个位置都是1，有1种排法，由此利用分步计数原理得满足条件的数列{an}的个数．
解答 解：∵数列{an}共有六项，其中四项是1，其余两项各不相同，
∴先排各不相同的两项，有${A}_{6}^{2}$种排法，其余4个位置都是1，有1种排法，
∴由分步计数原理得满足条件的数列{an}共有：${A}_{6}^{2}×1$=30个．
故选：A．
点评 本题考查满足条件的数列的个数的求法，是基础题，解题时要认真审题，注意排列组合知识的合理运用．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
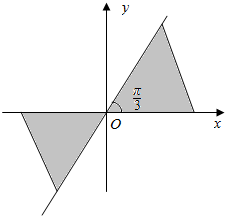如图所示，阴影部分表示的角的集合为（含边界）{α|kπ≤α≤kπ+$\frac{π}{3}$，k∈Z}（用弧度表示）．