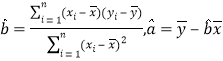题目内容
【题目】已知函数![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明:
时,证明:![]()
【答案】(1)递减区间为(-1,0),递增区间为![]() (2)见解析
(2)见解析
【解析】
(1)根据函数解析式,先求得导函数,由![]() 是函数
是函数![]() 的极值点可求得参数
的极值点可求得参数![]() .求得函数定义域,并根据导函数的符号即可判断单调区间.
.求得函数定义域,并根据导函数的符号即可判断单调区间.
(2)当![]() 时,
时,![]() .代入函数解析式放缩为
.代入函数解析式放缩为![]() ,代入证明的不等式可化为
,代入证明的不等式可化为![]() ,构造函数
,构造函数![]() ,并求得
,并求得![]() ,由函数单调性及零点存在定理可知存在唯一的
,由函数单调性及零点存在定理可知存在唯一的![]() ,使得
,使得![]() 成立,因而求得函数
成立,因而求得函数![]() 的最小值
的最小值![]() ,由对数式变形化简可证明
,由对数式变形化简可证明![]() ,即
,即![]() 成立,原不等式得证.
成立,原不等式得证.
(1)函数![]()
可求得![]() ,则
,则![]()
解得![]()
所以![]() ,定义域为
,定义域为![]()
![]() ,
,
![]() 在
在![]() 单调递增,而
单调递增,而![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
此时![]() 是函数
是函数![]() 的极小值点,
的极小值点,
![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]()
(2)证明:当![]() 时,
时,![]()
![]() ,
,
因此要证当![]() 时,
时,![]() ,
,
只需证明![]() ,
,
即![]()
令![]() ,
,
则![]() ,
,
![]() 在
在![]() 是单调递增,
是单调递增,
而![]() ,
,
∴存在唯一的![]() ,使得
,使得![]() ,
,
当![]() ,
,![]() 单调递减,当
单调递减,当![]() ,
,![]() 单调递增,
单调递增,
因此当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() ,
,
![]() ,
,
![]() ,
,
故![]() ,
,
从而![]() ,即
,即![]() ,结论成立.
,结论成立.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
【题目】为大力提倡“厉行节约,反对浪费”,衡阳市通过随机询问100名性别不同的居民是否做到“光盘”行动,得到如右列联表及附表:经计算: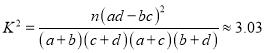 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
|
|
|
|
k |
|
|
|
A.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别无关”
C.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关”
D.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关”