题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,当
上单调递增,当![]() 时,
时, ![]() 的
的![]() 上单调递增.(2)
上单调递增.(2)![]() 或
或![]() .
.
【解析】试题分析:(1)先求函数导数,并因式分解![]() ,安装导函数是否变号进行分类讨论:当
,安装导函数是否变号进行分类讨论:当![]() 时,导函数不变号,在定义区间上单调递增;当
时,导函数不变号,在定义区间上单调递增;当![]() 时,导函数由负变正,单调性先减后增(2)构造差函数
时,导函数由负变正,单调性先减后增(2)构造差函数![]() ,结合(1)讨论
,结合(1)讨论![]() 单调性,确定对应最小值,解出对应
单调性,确定对应最小值,解出对应![]() 的取值范围.
的取值范围.
试题解析:解:(1)![]() ,定义域为
,定义域为![]() ,
,
![]() .
.
①当![]() ,即
,即![]() 时,令
时,令![]() , ∵
, ∵![]() ,∴
,∴![]() ,
,
令![]() , ∵
, ∵![]() , ∴
, ∴![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() 恒成立,
恒成立,
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 的
的![]() 上单调递增.
上单调递增.
(2)由题意可知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,
成立,
即在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,
即函数![]() 在
在![]() 上的最小值
上的最小值![]() .
.
由(1)知,①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() , ∴
, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增, ∴
上单调递增, ∴![]() , ∴
, ∴![]() ;
;
③当![]() ,即
,即![]() 时, ∴
时, ∴![]() ,
,
∵![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
此时不存在![]() 使
使![]() 成立,
成立,
综上可得![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

【题目】拉丁舞,又称拉丁风情舞或自由社交舞,它是拉丁人民在漫长的历史长河中形成的,包含伦巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜爱.某艺术培训机构为了调查本校学院对拉丁舞的学习情况,分别在刚学习了一个季度的本校大班(8岁以下)及种子班(8岁以上)的学员中各随机抽取了15名学员进行摸底考试,这30名学员考试成绩的茎叶图如图所示.

规定:成绩不低于85分,则认为成绩优秀;成绩低于85分,则认为成绩一般.
(1)根据上述数据填写下列2×2联表:
成绩优秀 | 成绩一般 | 总计 | |
大班 | |||
种子班 | |||
总计 |
判断是否有95%的把握认为成绩优秀或成绩一般与学员的年龄有关;
(2)在大班及种子班的参加摸底考试且成绩优秀的学员中以分层抽样的方式抽取6名学员进行特别集训,集训后,再对这6名学员进行测试,按测试成绩,取前3名授予“舞蹈小精灵”称号,在被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率.
参考公式及数据: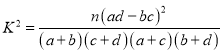 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |