Question

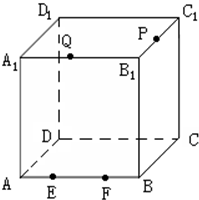在棱长为a的正方体ABCD-A₁B₁C₁D₁中，P是C₁B₁的中点，若E，F都是AB上的点，且|EF|=

a

2

，Q是A₁B₁上的点，则四面体EFPQ的体积是

 

．

Answer 1

分析：由已知中棱长为a的正方体ABCD-A₁B₁C₁D₁中，P是C₁B₁的中点，若E，F都是AB上的点，且|EF|=

a

2

，Q是A₁B₁上的点，我们分别计算出四面体EFPQ的底面面积S_△EFQ和高，代入棱锥体积公式，即可得到答案．

解答：解：∵棱长为a的正方体ABCD-A₁B₁C₁D₁中，
又∵E，F都是AB上的点，且|EF|=

a

2

，Q是A₁B₁上的点，
∴S_△EFQ=

1

2

•EF•BB₁=

a 2

4

又∵P是C₁B₁的中点，
∴四面体EFPQ的高为

a

2

∴四面体EFPQ的体积V=

1

3

•Sh=

1

3

•

a 2

4

•

a

2

=

a3

24

故答案为：

a3

24

点评：本题考查的知识点是棱锥的体积，其中计算出棱锥的底面面积和高，是解答本题的关键，本题是一个运动变化题，要从动中求静，找到变化过程中，不变的量，进行解答．