Question

在棱长为a的正方体ABCD-A₁B₁C₁D₁中，向量

BA1

与向量

AC

所成的角为

120°

．

Answer 1

分析：先建立空间直角坐标系，求出向量

BA1

与

AC

的坐标，然后利用空间向量的夹角公式进行运算即可．

解答：解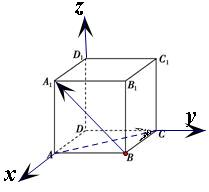：建立如图所示的空间直角坐标系
则A（a，0，0），B（a，a，0），C（0，a，0），A₁（a，0，a）
∴

BA1

=（0，-a，a），

AC

=（-a，a，0）
∴cos＜

BA1

，

AC

＞=

AC • BA1

| AC |×| BA1 |

=

-a2

2 a× 2 a

=-

1

2

即＜

BA1

，

AC

＞=120°
故答案为：120°

点评：本题主要考查了利用空间向量求夹角，解题的关键熟练掌握空间向量的夹角公式，属于基础题．