题目内容

在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别为A1B和CC1的中点.求:
(Ⅰ)直线MN和BC所成角的正切值;
(Ⅱ)直线A1B和平面ABCD所成角的大小;
(Ⅲ)点N到直线AB的距离.
分析:(Ⅰ)取BB1中点E,连接MN,NE,ME,根据中点得EN∥BC,然后在RT△MNE中求出tan∠MNE即可;
(Ⅱ)根据原图是棱长为a的正方体ABCD-A1B1C1D1,可直接得到∠A1BA即为直线A1B和平面ABCD所成角,再求出∠A1BA即可;
(Ⅲ)连接BN,根据原图是棱长为a的正方体ABCD-A1B1C1D1,先得到 AB⊥面BCC1B1,进而得 AB⊥BN,得BN的长即为点N到直线AB的距离,然后在RT△BCN中,求出BN即可.
(Ⅱ)根据原图是棱长为a的正方体ABCD-A1B1C1D1,可直接得到∠A1BA即为直线A1B和平面ABCD所成角,再求出∠A1BA即可;
(Ⅲ)连接BN,根据原图是棱长为a的正方体ABCD-A1B1C1D1,先得到 AB⊥面BCC1B1,进而得 AB⊥BN,得BN的长即为点N到直线AB的距离,然后在RT△BCN中,求出BN即可.
解答:解:取BB1中点E,连接MN,NE,ME.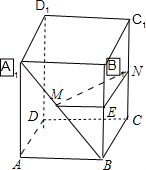
(Ⅰ)∵E,N分别为BB1,CC1
∴EN∥BC,
∴∠MNE或其补角即为直线MN和BC所成角,
又∵M,E也分别为对应边的中点,
所以 ME∥AB.
又因为AB⊥BC.
∴ME⊥EN,在RT△MNE中,tan∠MNE=
=
=
.
故直线MN和BC所成角的正切值为
.
(Ⅱ)∵原图是棱长为a的正方体ABCD-A1B1C1D1
∴∠A1BA即为直线A1B和平面ABCD所成角.
又因为 A1A⊥AB,A1A=AB.
∴∠A1BA=45°.
故直线A1B和平面ABCD所成角为45°
(Ⅲ)连接BN,
∵原图是棱长为a的正方体ABCD-A1B1C1D1
所以 AB⊥面BCC1B1,
∴AB⊥BN.
故BN的长即为点N到直线AB的距离,
在RT△BCN中,BN=
=
=
a.
所以点N到直线AB的距离为
a

(Ⅰ)∵E,N分别为BB1,CC1
∴EN∥BC,
∴∠MNE或其补角即为直线MN和BC所成角,
又∵M,E也分别为对应边的中点,
所以 ME∥AB.
又因为AB⊥BC.
∴ME⊥EN,在RT△MNE中,tan∠MNE=
| ME |
| NE |
| ||
| a |
| 1 |
| 2 |
故直线MN和BC所成角的正切值为
| 1 |
| 2 |
(Ⅱ)∵原图是棱长为a的正方体ABCD-A1B1C1D1
∴∠A1BA即为直线A1B和平面ABCD所成角.
又因为 A1A⊥AB,A1A=AB.
∴∠A1BA=45°.
故直线A1B和平面ABCD所成角为45°
(Ⅲ)连接BN,
∵原图是棱长为a的正方体ABCD-A1B1C1D1
所以 AB⊥面BCC1B1,
∴AB⊥BN.
故BN的长即为点N到直线AB的距离,
在RT△BCN中,BN=
| BC2+CN2 |
a2+(
|
| ||
| 2 |
所以点N到直线AB的距离为
| ||
| 2 |
点评:本题是对立体几何知识的综合考查,涉及到线线角以及线面角的求法和点到直线的距离问题,在求直线和直线所成角时,一般是通过平移,把问题转化到在一个三角形中求两边的夹角问题.

练习册系列答案
相关题目
