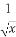题目内容
若a,b在区间[0,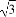 ]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
(A) (B)
(B)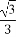 (C)
(C)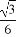 (D)1-
(D)1-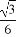
C
【解析】【思路点拨】f(x)在R上有两个相异极值点的充要条件是a≠0且其导函数的判别式大于0.
解:易得f'(x)=3ax2+2bx+a,函数f(x)=ax3+bx2+ax在R上有两个相异极值点的充要条件是a≠0且其导函数的判别式大于0,即a≠0且4b2-12a2>0.又a,b在区间[0,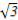 ]上取值,则a>0,b>
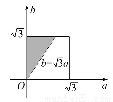
]上取值,则a>0,b>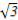 a,满足点(a,b)的区域如图中阴影部分所示,其中正方形区域的面积为3,阴影部分的面积为
a,满足点(a,b)的区域如图中阴影部分所示,其中正方形区域的面积为3,阴影部分的面积为 ,故所求的概率是
,故所求的概率是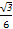 .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目