题目内容
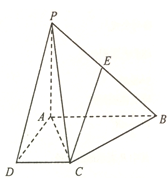
【题目】如图,四棱锥![]() 中,
中, ![]() ,侧面
,侧面![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() .
.
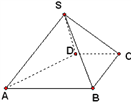
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
【答案】(1)见解析(2)![]()
【解析】试题分析:(Ⅰ)由问题,可根据线面垂直判定定理的条件要求,从题目条件去寻相关的信息,先证线线垂直,即![]() ,从而问题可得解;(Ⅱ)要求直线与平面所成角,一般步骤是先根据图形特点作出所求的线面角,接着将该所在三角形的其他要素(包括角、边或是三角形的形状等)算出来,再三角形的性质或是正弦定理、余弦定理来进行运算,从问题得于解决(类似问题也可以考虑采用坐标法来解决).
,从而问题可得解;(Ⅱ)要求直线与平面所成角,一般步骤是先根据图形特点作出所求的线面角,接着将该所在三角形的其他要素(包括角、边或是三角形的形状等)算出来,再三角形的性质或是正弦定理、余弦定理来进行运算,从问题得于解决(类似问题也可以考虑采用坐标法来解决).
试题解析:(Ⅰ)取![]() 的中点E,连接
的中点E,连接![]() ,
,
则四边形![]() 为矩形,
为矩形,
所以![]() ,
,
所以![]() ,
,
因为侧面![]() 为等边三角形,
为等边三角形, ![]() ,
,
所以![]() ,且
,且![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)
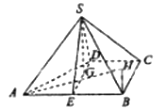
过点![]() 作
作![]() ⊥
⊥![]() 于点
于点![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
由平面与平面垂直的性质,
知![]() 平面
平面![]() ,
,
在![]() 中,由
中,由![]() ,
,
得![]() ,
,
所以![]() .
.
过点![]() 作
作![]() 平面
平面![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() 即为
即为![]() 与平面
与平面![]() 所成的角,
所成的角,
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
在![]() 中,由
中,由![]() ,
,
求得![]() .
.
在![]() 中,
中, ![]() ,
,
所以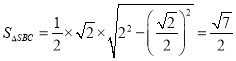 ,
,
由![]() ,
,
得![]() ,
,
即![]() ,
,
解得![]() ,
,
所以![]() ,
,
故![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.