题目内容
12.已知函数f(x)=ex-x2,g(x)=ax+b(a>0),若对?x1∈[0,2],?x2∈[0,2],使得f(x1)=g(x2),则实数a,b的取值范围是( )| A. | 0<a≤$\frac{{{e^2}-5}}{2}$,b≥1 | B. | 0<a≤$\frac{{{e^2}-5}}{2}$,b≤1 | C. | a≥$\frac{{{e^2}-5}}{2}$,b≥1 | D. | a≥$\frac{{{e^2}-5}}{2}$,b≤1 |
分析 对?x1∈[0,2],?x2∈[0,2],使得f(x1)=g(x2),等价于x∈[0,2]时f(x)的值域为g(x)值域的子集,利用单调性求得两函数的值域,由集合的包含关系可得不等式,解出即可.
解答 解:因为f′(x)=ex-2x,
令y=ex-2x,可得y′=ex-2,令ex-2=0,解得x=ln2,
y=ex-2x的最小值为:2ln2-2ln2=2-2ln2>0
可得f′(x)=ex-2x>0,所以f(x)在[0,2]上递增,
所以x∈[0,2]时,f(0)≤f(x)≤f(2),即1≤f(x)≤e2-2,
由a>0得g(x)=ax+b在[0,2]上递增,
所以x∈[0,2]时,g(0)≤g(x)≤g(2),即b≤g(x)≤2a+b,
又对?x1∈[0,2],?x2∈[0,2],使得f(x1)=g(x2),
所以有[1,e2-4]⊆[b,2a+b],则$\left\{\begin{array}{l}b≤1\\ 2a+b>{e}^{2}-4\end{array}\right.$,
由e2-4-2a≤b≤1得,a≥$\frac{{e}^{2}-5}{2}$,
故选:D.
点评 本题考查利用导数求函数在闭区间上的最值、函数单调性的应用,考查恒成立问题,本题中对恒成立问题的等价转化是解决问题的关键.

练习册系列答案
相关题目
1.下边是某个学生在学习《函数的最值》一节以后做的作业,其解答过程和结论都是正确的,但是不知道什么原因,题目中定义域部分[0,█]看不清楚,请你根据所学的只是,判断一下图中“█”的可能取值.
| 已知函数y=x2-3x-4 |
| 定义域为[0,█],求函数的值域 |
| 解:… |
| … |
| … |
| … |
| … |
| 故函数的值域为[-$\frac{25}{4}$,-4] |
20.函数y=$\frac{1-a}{x}$(a≠1)在(-∞,0),(0,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
7.在复平面内,已知复数z=$\frac{i}{1-i}$,则其共轭复数$\overline z$的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
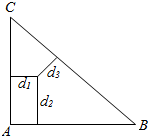 点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].
点P在△ABC内部(包含边界),|AC|=3,|AB|=4,|BC|=5,点P到三边的距离分别是d1,d2,d3,则d1+d2+d3的取值范围是[$\frac{12}{5}$,4].