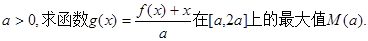题目内容
(13分)
已知函数![]()
(I)当a<0时,求函数![]() 的单调区间;
的单调区间;
(II)若函数f(x)在[1,e]上的最小值是![]() 求a的值.
求a的值.
(13分)
解:函数![]() 的定义域为
的定义域为![]() …………1分
…………1分
![]() …………3分
…………3分
(1)![]()
故函数在其定义域![]() 上是单调递增的. …………5分
上是单调递增的. …………5分
(II)在[1,e]上,发如下情况讨论:
①当a<1时,![]() 函数
函数![]() 单调递增,
单调递增,
其最小值为![]()
这与函数在[1,e]上的最小值是![]() 相矛盾; …………6分
相矛盾; …………6分
②当a=1时,函数![]() 单调递增,
单调递增,
其最小值为![]()
同样与最小值是![]() 相矛盾; …………7分
相矛盾; …………7分
③当![]() 时,函数
时,函数![]() 上有
上有![]() ,单调递减,
,单调递减,
在![]() 上有
上有![]() 单调递增,所以,
单调递增,所以,
函数![]() 满足最小值为
满足最小值为![]() www..co
www..co
由![]() …………9分
…………9分
④当a=e时,函数![]() 单调递减,
单调递减,
其最小值为![]() 还与最小值是
还与最小值是![]() 相矛盾; …………10分
相矛盾; …………10分
⑤当a>e时,显然函数![]() 上单调递减,
上单调递减,
其最小值为![]()
仍与最小值是![]() 相矛盾; …………12分
相矛盾; …………12分
综上所述,a的值为![]() …………13分
…………13分

练习册系列答案
相关题目
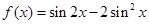
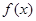 的最小正周期。
的最小正周期。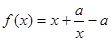
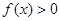 对任意
对任意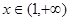 恒成立,求实数
恒成立,求实数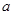 的取值范围;
的取值范围;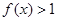 .
.
 处的切线的方程;
处的切线的方程;