题目内容
已知抛物线y2=2px(p>0)的焦点为F,过F的直线交y轴正半轴于点P,交抛物线于A,B两点,其中点A在第一象限,若 ,
,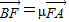 ,
,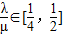 ,则μ的取值范围是( )
,则μ的取值范围是( )A.

B.
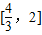
C.[2,3]
D.[3,4]
【答案】分析:设P(0,y),B(x2,y2),A(x1,y1),代入已知向量式,由向量相等的定义得A、B两点横坐标与纵坐标间的关系,再结合两点在抛物线上,经互相代换得λ和μ间的等式,从而利用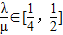 求得μ的范围
求得μ的范围
解答:解:设P(0,y),B(x2,y2),A(x1,y1),由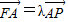 ,
,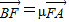
得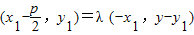 ,
,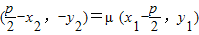
∴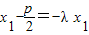 ,y1=λ(y-y1),
,y1=λ(y-y1),
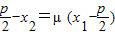 ,y2=-μy1,
,y2=-μy1,
∴y22=μ2y12,
∵y12=2px1,y22=2px2.
∴x2=μ2x1,
代入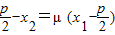
得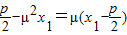 ,即
,即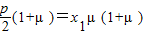
整理,得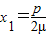
代入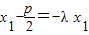 ,得
,得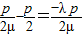
∴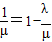
∵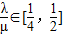
∴ ∈[
∈[ ,
, ]
]
∴μ∈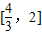
故选 B
点评:本题主要考查了直线与抛物线的关系,向量与解析几何的综合应用,求变量取值范围问题的解法,利用已知向量式得到λ和μ间的等式是解决问题的关键
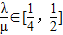 求得μ的范围
求得μ的范围解答:解:设P(0,y),B(x2,y2),A(x1,y1),由
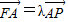 ,
,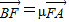
得
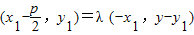 ,
,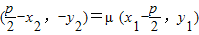
∴
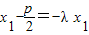 ,y1=λ(y-y1),
,y1=λ(y-y1),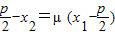 ,y2=-μy1,
,y2=-μy1,∴y22=μ2y12,
∵y12=2px1,y22=2px2.
∴x2=μ2x1,
代入
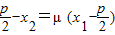
得
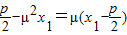 ,即
,即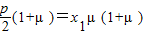
整理,得
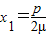
代入
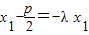 ,得
,得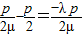
∴
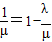
∵
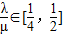
∴
 ∈[
∈[ ,
, ]
]∴μ∈
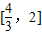
故选 B
点评:本题主要考查了直线与抛物线的关系,向量与解析几何的综合应用,求变量取值范围问题的解法,利用已知向量式得到λ和μ间的等式是解决问题的关键

练习册系列答案
相关题目