题目内容
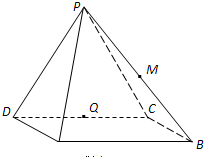 四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是∠ADC=60°的菱形,M为PB的中点,Q为CD的中点.
四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是∠ADC=60°的菱形,M为PB的中点,Q为CD的中点.(1)求证:PA⊥CD;
(2)求AQ与平面CDM所成的角.
分析:(1)连结PQ、AQ.菱形ABCD中证出AQ⊥CD,结合正三角形△PCD中PQ⊥CD,可得CD⊥平面PAQ,而PA?平面PAQ,即可证出PA⊥CD.
(2)分别以QA、QC、QP所在直线为x、y、z轴,建立如图空间直角坐标系Q-xyz.算得
、
的坐标,从而得到
?
=0,可得PA⊥CM.结合(1)的结论PA⊥CD,证出PA⊥平面CDM,得
就是平面CDM的法向量.因此根据空间向量的夹角公式算出<
,
>的余弦值,即可得到AQ与平面CDM所成的正弦值,从而求出AQ与平面CDM所成的角的大小.
(2)分别以QA、QC、QP所在直线为x、y、z轴,建立如图空间直角坐标系Q-xyz.算得
| PA |
| CM |
| PA |
| CM |
| PA |
| QA |
| PA |
解答:解:(1)连结PQ、AQ.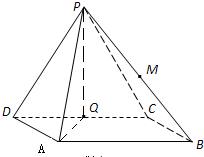
∵△PCD为正三角形,∴PQ⊥CD.
∵底面ABCD是∠ADC=60°的菱形,
∴AQ⊥CD.
∵AQ、PQ是平面PAQ内的相交直线,
∴CD⊥平面PAQ.…(4分)
∵PA?平面PAQ,∴PA⊥CD.
(2)由(1)可知PQ⊥CD,AQ⊥CD.
又由侧面PDC⊥底面ABCD,得PQ⊥AQ.
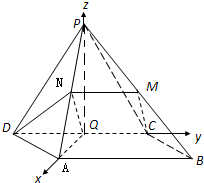
因此,分别以QA、QC、QP所在直线为x、y、z轴,建立如图空间直角坐标系Q-xyz.…(6分)
易知P(0,0,
)、A(
,0,0)、B(
,2,0)、C(0,1,0)、D(0,-1,0).…(7分)
由M(
,1,
),得
=(
,0,
),
得
?
=
+0-
=0,可得PA⊥CM.…(10分)
∵CM、CD是平面CDM内的相交直线,
∴PA⊥平面CDM,
从而
就是平面CDM的法向量.…(12分)
设AQ与平面所成的角为α,
则sinα=|cos<
,
>|=|
|=
,可得α=45°
∴AQ与平面CDM所成的角为45°.…(14分)

∵△PCD为正三角形,∴PQ⊥CD.
∵底面ABCD是∠ADC=60°的菱形,
∴AQ⊥CD.
∵AQ、PQ是平面PAQ内的相交直线,
∴CD⊥平面PAQ.…(4分)
∵PA?平面PAQ,∴PA⊥CD.
(2)由(1)可知PQ⊥CD,AQ⊥CD.
又由侧面PDC⊥底面ABCD,得PQ⊥AQ.
因此,分别以QA、QC、QP所在直线为x、y、z轴,建立如图空间直角坐标系Q-xyz.…(6分)
易知P(0,0,
| 3 |
| 3 |
| 3 |
由M(
| ||
| 2 |
| ||
| 2 |
| CM |
| ||
| 2 |
| ||
| 2 |

得
| PA |
| CM |
| 3 |
| 4 |
| 3 |
| 4 |
∵CM、CD是平面CDM内的相交直线,
∴PA⊥平面CDM,
从而
| PA |
设AQ与平面所成的角为α,
则sinα=|cos<
| QA |
| PA |
| 3 | ||||
|
| ||
| 2 |
∴AQ与平面CDM所成的角为45°.…(14分)
点评:本题在特殊四棱锥中求证异面垂直,并求直线与平面所成角的大小,着重考查了线面垂直的判定与性质、利用空间向量研究直线与平面所成角大小等知识,属于中档题.

练习册系列答案
相关题目
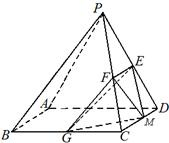 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.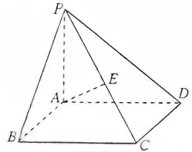 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2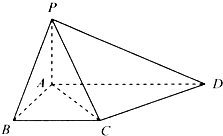 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.