题目内容
设集合A={x|0≤x≤1},B={x|0≤x≤2},下面的对应中,是从A到B的函数的是( )
| A.f:x®3x | B.f:x®x2 | C.f:x®± | D.f:x®2.5 |
B
在f:x→3x中,当集合A中x=1时,对应的3x=3在集合B中不存在,
∴选项A不成立;
在f:x→x2中,集合A的所有x值,在集合B中都有唯一的元素与之相对应,
故选B成立;
在f:x→± 中,不满足函数的单值对应的性质,故选项C不成立;
中,不满足函数的单值对应的性质,故选项C不成立;
在f:x→2.5中,对于集合A中的x,对应的2.5在集合B中不存在,
故选项D不成立.
故选B.
∴选项A不成立;
在f:x→x2中,集合A的所有x值,在集合B中都有唯一的元素与之相对应,
故选B成立;
在f:x→±
 中,不满足函数的单值对应的性质,故选项C不成立;
中,不满足函数的单值对应的性质,故选项C不成立;在f:x→2.5中,对于集合A中的x,对应的2.5在集合B中不存在,
故选项D不成立.
故选B.

练习册系列答案
相关题目
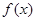 满足
满足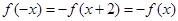 ,当
,当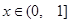 时
时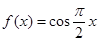 ,那么在
,那么在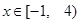 上方程
上方程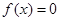 的所有根的和是
的所有根的和是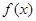 ,对任意
,对任意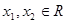 ,恒有
,恒有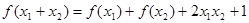 ,求:(1)
,求:(1)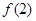 的值;(2)
的值;(2)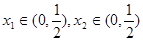 ,都有
,都有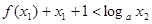 成立时,求
成立时,求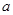 的取值范围.
的取值范围.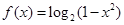 的定义域为
的定义域为  上的函数
上的函数 满足
满足 且
且 时,
时, ,则
,则 ( )
( )


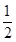 )x-1.
)x-1.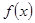 是定义在
是定义在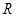 上的奇函数,
上的奇函数,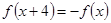 ,且在
,且在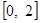 上
上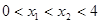 且
且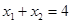 ,则
,则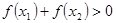 ;
;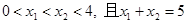 ,则
,则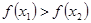 ;③若方程
;③若方程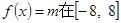 内恰有四个不同的解
内恰有四个不同的解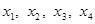 ,则
,则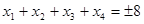 。
。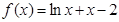 的零点在下列哪个区间内( )
的零点在下列哪个区间内( )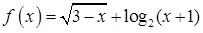 的定义域为 ( )
的定义域为 ( )


