题目内容
在区间[-6,6]内任取一个元素x,若抛物线y=x2在x=x处的切线的倾角为α,则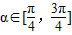 的概率为 .
的概率为 .
【答案】分析:由倾斜角α的范围,可以得出曲线的斜率的范围,再由导数的几何意义求出x的范围,进而求出x所在区间的长度,最后得出答案.
解答:解:当α∈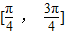 时,切线的斜率k≥1或k≤-1,
时,切线的斜率k≥1或k≤-1,
又 y′=2x,所以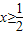 或
或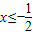 ,
,
∴[-6,6]∩((-∞,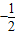 ]∪[
]∪[ ,+∞))=
,+∞))=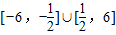 ,
,
∴点x所在区间的长度=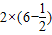 =11,区间[-6,6]的长度=12,
=11,区间[-6,6]的长度=12,
所以P=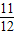 .
.
故答案为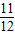 .
.
点评:正确求出x满足的区间长度是解题的关键.
解答:解:当α∈
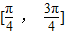 时,切线的斜率k≥1或k≤-1,
时,切线的斜率k≥1或k≤-1,又 y′=2x,所以
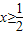 或
或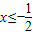 ,
,∴[-6,6]∩((-∞,
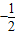 ]∪[
]∪[ ,+∞))=
,+∞))=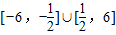 ,
,∴点x所在区间的长度=
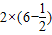 =11,区间[-6,6]的长度=12,
=11,区间[-6,6]的长度=12,所以P=
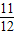 .
.故答案为
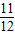 .
.点评:正确求出x满足的区间长度是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
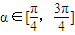 的概率为 .
的概率为 .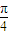 ,
,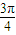 ]的概率为 .
]的概率为 .