题目内容
在区间[-6，6]内任取一个元素x，抛物线x2=4y在x=x处的切线的倾斜角为α，则α∈[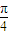
，
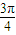]的概率为 ．
【答案】分析：求出导函数在[-6，6]的范围，就是切线的斜率的范围，通过切线的倾斜角为α，α∈[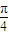
，
]求出斜率的范围，利用几何概型求出概率．
解答：解：由题意可知x2=4y的导数为：y′=
x，在区间x∈[-6，6]，切线的斜率为：[-3，3]．
倾斜角为α，α∈[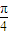
，
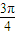]，斜率范围是[1，+∞）∪（-∞，-1]，
α的斜率在[-3，3]内的部分是[-3，-1]∪[1，3]．
所以满足题意的概率为：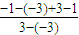
=
．
故答案为：
．
点评：本题考查几何概型的应用，正确理解题意是解题的关键．
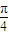，]求出斜率的范围，利用几何概型求出概率．解答：解：由题意可知x2=4y的导数为：y′=
x，在区间x∈[-6，6]，切线的斜率为：[-3，3]．倾斜角为α，α∈[
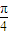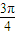，]，斜率范围是[1，+∞）∪（-∞，-1]，α的斜率在[-3，3]内的部分是[-3，-1]∪[1，3]．
所以满足题意的概率为：
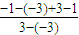=．故答案为：
．点评：本题考查几何概型的应用，正确理解题意是解题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
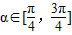的概率为 ．
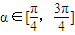的概率为 ．