题目内容
【题目】设不等式mx2－2x－m＋1＜0对于满足|m|≤2的一切m的值都成立，求x的取值范围．
【答案】
【解析】
令f（m）=m（x2﹣1）﹣2x+1，由条件f（m）＜0对满足|m|≤2的一切m的值都成立，利用一次函数的单调性可得：f（﹣2）＜0，f（2）＜0．解出即可．
令f（m）=m（x2﹣1）﹣2x+1，由条件f（m）＜0对满足|m|≤2的一切m的值都成立，
则需要f（﹣2）＜0，f（2）＜0．
解不等式组
，解得，
∴x的取值范围是．
【点睛】
本题考查了一次函数的单调性、一元二次不等式的解法，考查了转化方法，考查了推理能力与计算能力，属于中档题．
【题型】解答题
【结束】
21
【题目】某厂有一批长为18m的条形钢板，可以割成1.8m和1.5m长的零件．它们的加工费分别为每个1元和0.6元．售价分别为20元和15元，总加工费要求不超过8元．问如何下料能获得最大利润.
【答案】只要截
长的零件12个，就能获得最大利润
【解析】
先画出满足条件的平面区域，求出M的坐标，找出M附近的点的坐标，代入求出即可．
设割成的1.8m和1.5m长的零件分别为x个、y个，利润为z元，
则z=20x+15y﹣（x+0.6y）即z=19x+14.4y且
，
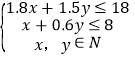作出不等式组表示的平面区域如图：
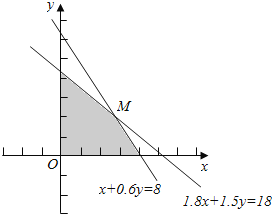
由
，解得：M（
，
），
∵x、y为自然数，在可行区域内找出与M最近的点为（3，8），此时z=19×3+14.4×8=172.2（元），
又可行域的另一顶点是（0，12），过（0，12）的直线使z=19×0+14.4×12=172.8（元），
过顶点（8，0）的直线使z=19×8+14.4×0=152（元），
M（7（20），7（60））附近的点（1，10）、（2，9），
直线z=19x+14.4y过点（1，10）时，z=163；过点（2，9）时z=167.6，
∴当x=0，y=12时，z=172.8元为最大值；
答：只要截1.5m长的零件12个，就能获得最大利润．
阅读快车系列答案
