题目内容
数列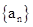 的通项公式为
的通项公式为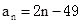 ,当该数列的前
,当该数列的前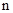 项和
项和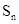 达到最小时,
达到最小时,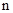 等于( )
等于( )
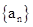 的通项公式为
的通项公式为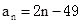 ,当该数列的前
,当该数列的前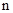 项和
项和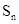 达到最小时,
达到最小时,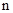 等于( )
等于( )A.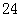 | B.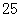 | C.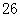 | D. |
A
试题分析:先由an=2n-49,判断数列{an}为等差数列,从而Sn =n2-48n,结合二次函数的性质可求.解:由an=2n-49可得an+1-an=2(n+1)-49-(2n-49)=2是常数,∴数列{an}为等差数列,从而
 故可知 Sn =n2-48n,结合二次函数的性质可得,当n=24时,和Sn有最小值.故答案为A
故可知 Sn =n2-48n,结合二次函数的性质可得,当n=24时,和Sn有最小值.故答案为A点评:本题的考点是等差数列的通项公式,主要考查了等差数列的求和公式的应用,解题时要认真审题,仔细解答,注意数列的函数性质的应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
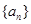 的前n项和为
的前n项和为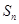 ,若
,若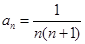 ,则
,则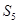 等于( )
等于( )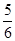
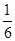
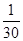
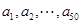 是从-1,0,1这三个整数中取值的数列,若
是从-1,0,1这三个整数中取值的数列,若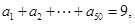
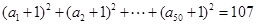 ,则
,则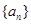 的首项
的首项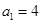 ,且
,且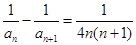 (
(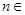 N*),数列
N*),数列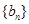 的前
的前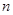 项和
项和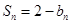 。
。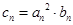 ,证明:当且仅当
,证明:当且仅当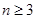 时,
时,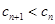 。
。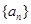 的前
的前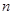 项和为
项和为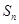 ,且有
,且有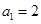 ,
,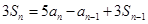
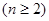 .
.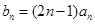 ,求数列
,求数列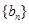 的前
的前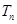 ;
;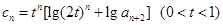 ,且数列
,且数列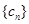 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数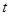 的取值范围.
的取值范围.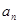 }中,若对任意的n均有
}中,若对任意的n均有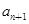 +
+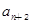 为定值
为定值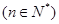 ,且
,且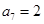 ,
,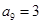 ,
,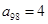 则数列
则数列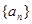 的前n项和为
的前n项和为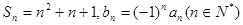 ,则数列
,则数列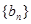 的前50项的和为( )
的前50项的和为( )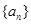 中,
中,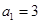 ,
,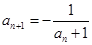 (
(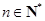 ),能使
),能使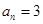 的
的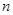 可以等于( ).
可以等于( ).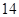
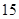
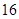
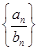 的前n项和T.
的前n项和T.