题目内容
已知箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4.
(1)从箱子中任取两张卡片,求两张卡片的标号之和不小于5的概率;
(2)从箱子中任意取出一张卡片,记下它的标号 ,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号
,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号 ,求使得幂函数
,求使得幂函数 图像关于
图像关于 轴对称的概率.
轴对称的概率.
(1) (2)
(2)
解析试题分析:(1)首先求出从4张卡片中任取2张的取法数,然后再求出两张卡片的标号之和不小于5的取法数,最后根据随机事件的概率公式求解即可.
(2)求出数对 包含的基本事件个数,然后在求出使得幂函数
包含的基本事件个数,然后在求出使得幂函数 为偶函数的基本事件个数,最后根据随机事件的概率公式求解即可.
为偶函数的基本事件个数,最后根据随机事件的概率公式求解即可.
(1) (两张卡片的标号之和不小于5的概率)=
(两张卡片的标号之和不小于5的概率)=
 5分
5分
(2)数对 包含16个基本事件,(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) 8分
包含16个基本事件,(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4) 8分
其中使得幂函数 为偶函数的基本事件有(2,1),(2,3),(4,3)共3个基本事件,故
为偶函数的基本事件有(2,1),(2,3),(4,3)共3个基本事件,故 .
.
考点:随机事件的概率.

练习册系列答案
相关题目
李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
| 场次 | 投篮次数 | 命中次数 | 场次 | 投篮次数 | 命中次数 |
| 主场1 | 22 | 12 | 客场1 | 18 | 8 |
| 主场2 | 15 | 12 | 客场2 | 13 | 12 |
| 主场3 | 12 | 8 | 客场3 | 21 | 7 |
| 主场4 | 23 | 8 | 客场4 | 18 | 15 |
| 主场5 | 24 | 20 | 客场5 | 25 | 12 |
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记
 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较 与
与 的大小(只需写出结论)
的大小(只需写出结论) 为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
| 新能源汽车补贴标准 | |||
| 车辆类型 | 续驶里程 (公里) (公里) | ||
 |  |  | |
| 纯电动乘用车 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |  万元/辆 万元/辆 |
 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:| 分组 | 频数 | 频率 |
 |  |  |
 |  | 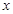 |
 |  |  |
| 合计 |  |  |
(1)求
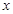 ,
, ,
, ,
, 的值;
的值;(2)若从这
 辆纯电动乘用车中任选
辆纯电动乘用车中任选 辆,求选到的
辆,求选到的 辆车续驶里程都不低于
辆车续驶里程都不低于 公里的概率;
公里的概率;(3)若以频率作为概率,设
 为购买一辆纯电动乘用车获得的补贴,求
为购买一辆纯电动乘用车获得的补贴,求 的分布列和数学期望
的分布列和数学期望 .
.  表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”.


 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求 ,求
,求 元,求
元,求