题目内容
15.已知α∈(-$\frac{π}{2}$,$\frac{3π}{2}$),tan(α-$\frac{π}{4}$)=-3,则sinα=±$\frac{\sqrt{5}}{5}$.分析 由条件利用同角三角函数的基本关系、两角差的正切公式求得tanα的值,可得sinα的值.
解答 解:α∈(-$\frac{π}{2}$,$\frac{3π}{2}$),tan(α-$\frac{π}{4}$)=$\frac{tanα-1}{1+tanα}$=-3,∴tanα=$\frac{sinα}{cosα}$=-$\frac{1}{2}$,
再根据sin2α+cos2α=1,求得sinα=$\frac{\sqrt{5}}{5}$,或sinα=-$\frac{\sqrt{5}}{5}$,
故答案为:±$\frac{\sqrt{5}}{5}$.
点评 本题主要考查同角三角函数的基本关系、两角差的正切公式,属于基础题.

练习册系列答案
相关题目
7.若a≤1,则$\sqrt{(a-1)^{2}}$化简后为( )
| A. | a-1 | B. | 1-a | C. | a+1 | D. | -a-1 |
4.设等差数列{an}的公差为d,若数列{2a1an}为递减数列,则( )
| A. | d<0 | B. | d>0 | C. | a1d<0 | D. | a1d>0 |
8.如图所示,M是△ABC的边AB的中点,若$\overrightarrow{CM}=\overrightarrow a,\overrightarrow{CA}$=$\overrightarrow b$,则$\overrightarrow{CB}$=( )
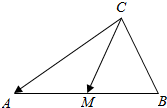

| A. | $\overrightarrow a-2\overrightarrow b$ | B. | $\overrightarrow a+2\overrightarrow b$ | C. | $2\overrightarrow a-\overrightarrow b$ | D. | $2\overrightarrow a+\overrightarrow b$ |