��Ŀ����
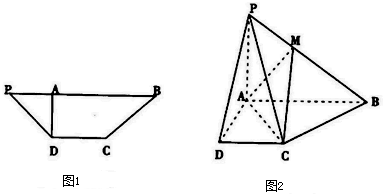 �ڵ�������PDCB��ͼ1���У�DC��PB��PB=3DC=3��PD=
�ڵ�������PDCB��ͼ1���У�DC��PB��PB=3DC=3��PD=| 2 |
��1��֤����ƽ��PAD��ƽ��PCD��
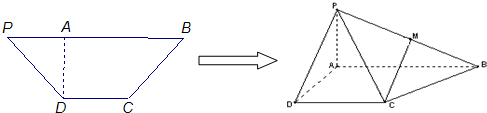
��2����M����PB�ϣ�ƽ��AMC������P-ABCD�ֳ����������壨��ͼ2����������������������֮��VPM-ACDVM-ABC=5��4ʱ����
| PM |
| MB |
��3���ڣ�2���������£�֤����PD��ƽ��AMC��
��������1����ͼ1��DA��PB���ɵ��۵���DA��AB��DA��PA������DC��PA��DC��DA�������洹ֱ���ж������õ�DC��ƽ��PAD���������洹ֱ���ж������õ�ƽ��PAD��ƽ��PCD��
��2����MN=h����ɵ�VM-ABC=
��VP-ABCD=
����VPM-ABCD=VP-ABCD-VM-ABC=
-
�����VPM-ABCD��VM-ABC=5��4�������hֵ�������õ�
��ֵ��
��3��������ABCD�У�����AC��BD���ڵ�O������OM����֪��AOB�ס�DOC��������ƽ��PBD�У���PD��MO������������ƽ�е��ж������õ��𰸣�
��2����MN=h����ɵ�VM-ABC=
| h |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| h |
| 3 |
| PM |
| MB |
��3��������ABCD�У�����AC��BD���ڵ�O������OM����֪��AOB�ס�DOC��������ƽ��PBD�У���PD��MO������������ƽ�е��ж������õ��𰸣�
���֤������1����Ϊ��ͼa�ĵ�������PDCB�У�DA��PB��
����������P-ABCD�У�DA��AB��DA��PA������1�֣�
��PA��AB����DC��AB������DC��PA��DC��DA������2�֣�
��DA?ƽ��PAD��PA?ƽ��PAD��PA��DA=A��
����DC��ƽ��PAD������3�֣�
��ΪDC?ƽ��PCD��
����ƽ��PAD��ƽ��PCD������4�֣�
�⣺��2����ΪDA��PA����PA��AB
����PA��ƽ��ABCD��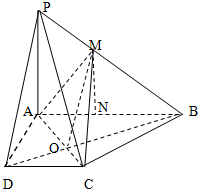
��PA?ƽ��PAB��
����ƽ��PAB��ƽ��ABC��
��ͼ����M��MN��AB������ΪN��
��MN��ƽ��ABCD������5�֣�
�ڵ�������PDCB�У�DC��PB��
PB=3DC=3��PD=
��DA��PB��
����PA=1��AB=2��AD=
=1������6�֣�
��MN=h����VM-ABC=
S��ABC•h=
������7�֣�
VP-ABCD=
S����ABCD•PA=
VPM-ABCD=VP-ABCD-VM-ABC=
-
������8�֣�
��ΪVPM-ABCD��VM-ABC=5��4��
���ԣ�
-
����
=5��4�����h=
������9�֣�
�ڡ�PAB�У�
=
=
������BM=
BP��MP=
BP��
����PM��MB=1��2������10�֣�
��3��������ABCD�У�����AC��BD���ڵ�O������OM��
��֪��AOB�ס�DOC������
=
=
������11�֣�
��PM��MB=1��2������
=
������12�֣�
������ƽ��PBD�У���PD��MO������13�֣�
����ΪPD?ƽ��AMC��MO?ƽ��AMC��
����PD��ƽ��AMC������14�֣�
����������P-ABCD�У�DA��AB��DA��PA������1�֣�
��PA��AB����DC��AB������DC��PA��DC��DA������2�֣�
��DA?ƽ��PAD��PA?ƽ��PAD��PA��DA=A��
����DC��ƽ��PAD������3�֣�
��ΪDC?ƽ��PCD��
����ƽ��PAD��ƽ��PCD������4�֣�
�⣺��2����ΪDA��PA����PA��AB
����PA��ƽ��ABCD��

��PA?ƽ��PAB��
����ƽ��PAB��ƽ��ABC��
��ͼ����M��MN��AB������ΪN��
��MN��ƽ��ABCD������5�֣�
�ڵ�������PDCB�У�DC��PB��
PB=3DC=3��PD=
| 2 |
����PA=1��AB=2��AD=
| PD2-PA2 |
��MN=h����VM-ABC=
| 1 |
| 3 |
| h |
| 3 |
VP-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
VPM-ABCD=VP-ABCD-VM-ABC=
| 1 |
| 2 |
| h |
| 3 |
��ΪVPM-ABCD��VM-ABC=5��4��
���ԣ�
| 1 |
| 2 |
| h |
| 3 |
| h |
| 3 |
| 2 |
| 3 |
�ڡ�PAB�У�
| BM |
| BP |
| MN |
| PA |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
����PM��MB=1��2������10�֣�
��3��������ABCD�У�����AC��BD���ڵ�O������OM��
��֪��AOB�ס�DOC������
| DO |
| OB |
| DC |
| AB |
| 1 |
| 2 |
��PM��MB=1��2������
| DO |
| OB |
| PM |
| MB |
������ƽ��PBD�У���PD��MO������13�֣�
����ΪPD?ƽ��AMC��MO?ƽ��AMC��
����PD��ƽ��AMC������14�֣�
���������⿼���֪ʶ����ƽ����ƽ�洹ֱ���ж���ֱ����ƽ��ƽ�е��ж�������������������տռ������ϵ���ж����������ʶ��������������ǽ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
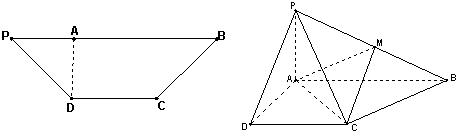
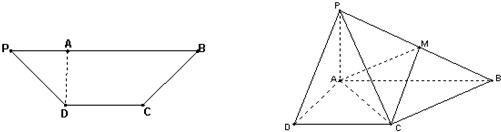
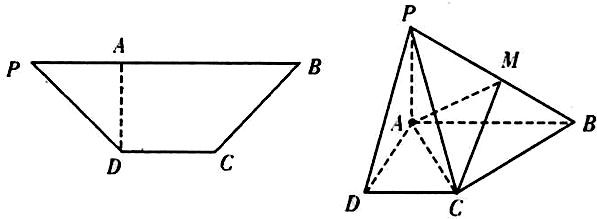
 ��2013•������ģ����ͼ���ڵ�������PDCB�У�PB��CD��PB=3��DC=1��PD=BC=
��2013•������ģ����ͼ���ڵ�������PDCB�У�PB��CD��PB=3��DC=1��PD=BC=