题目内容
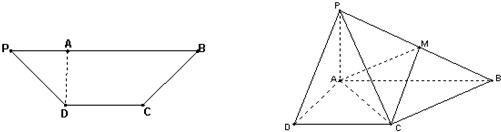
如图,在等腰梯形PDCB中,PB=3,DC=1,PD=BC=| 2 |
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)若M为PB的中点,试求异面直线AN和BC所成的角的余弦值.
(Ⅲ)试问:在侧棱PB上是否存在一点Q,使截面AQC把几何体分成的两部分的体积之比VPDCQA:VQACB=7:2?若存在,请求PQ的长;若不存在,请说明理由.
分析:(Ⅰ)由CD⊥AD和平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,根据面面垂直的性质定理证明;
(Ⅱ)如图,把四棱锥P-ABCD补成一个长方体,则有AM∥DF,DG∥CB,可得到∠FDG就是异面直线AM和BC所成的角,再在△GBE中,求得GE,在△GEF中,求得FG,在△FDG中,求得DG,利用由余弦定理求解.
(Ⅲ)假设在侧棱PB上存在一点Q,满足条件VPDCQA:VQACB=7:2,转化为
hS△ABC =
PASABCD,再由相似性求解.
(Ⅱ)如图,把四棱锥P-ABCD补成一个长方体,则有AM∥DF,DG∥CB,可得到∠FDG就是异面直线AM和BC所成的角,再在△GBE中,求得GE,在△GEF中,求得FG,在△FDG中,求得DG,利用由余弦定理求解.
(Ⅲ)假设在侧棱PB上存在一点Q,满足条件VPDCQA:VQACB=7:2,转化为
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
解答: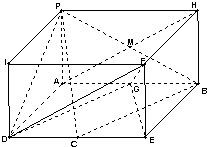 证明:(Ⅰ)依题意知PA=1,PD=
证明:(Ⅰ)依题意知PA=1,PD=
∴AD⊥AB,
又CD∥AB
∴CD⊥AD
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
CD⊥平面PAD(4分)
(Ⅱ)如图,把四棱锥P-ABCD补成一个长方体,
其中C,G分别为所在棱的中点,则易得AM∥DF,DG∥CB,
所以∠FDG就是异面直线AM和BC所成的角(6分)
连接FG,在△GBE中,GE=
=
在△GEF中,FG=
=
在△FDG中,DG=GE=
DF=
=
,
由余弦定理可得:
cos∠FDG=
=
(8分)
所以异面直线AM和BC所成的角的余弦值为
.(9分)
(Ⅲ)解:假设在侧棱PB上存在一点Q,满足条件
∵VPDCQA:VQACB=7:2
∴VQ-ACB=
VP-ABCD(11分)
又由∠PAD=∠DAB=90°知PA⊥平面ABCD,又
SABCD=
(DC+AB)AD=
,S△ABC=1.
设Q到平面ABCD的距离为h,则
hS△ABC =
PASABCD
∴h=
(12分)
又∵
=
,∴
=
故PQ=
PB=
(14分)
 证明:(Ⅰ)依题意知PA=1,PD=
证明:(Ⅰ)依题意知PA=1,PD=| 2 |
∴AD⊥AB,
又CD∥AB
∴CD⊥AD
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
CD⊥平面PAD(4分)
(Ⅱ)如图,把四棱锥P-ABCD补成一个长方体,
其中C,G分别为所在棱的中点,则易得AM∥DF,DG∥CB,
所以∠FDG就是异面直线AM和BC所成的角(6分)
连接FG,在△GBE中,GE=
| GB2+BE2 |
| 2 |
在△GEF中,FG=
| GE2+FE2 |
| 3 |
在△FDG中,DG=GE=
| 2, |
| DE2+FE2 |
| 5 |
由余弦定理可得:
cos∠FDG=
| DF2+DG2-FG2 |
| 2•DF•DG |
| ||
| 5 |
所以异面直线AM和BC所成的角的余弦值为
| ||
| 5 |
(Ⅲ)解:假设在侧棱PB上存在一点Q,满足条件
∵VPDCQA:VQACB=7:2
∴VQ-ACB=
| 2 |
| 9 |
又由∠PAD=∠DAB=90°知PA⊥平面ABCD,又
SABCD=
| 1 |
| 2 |
| 3 |
| 2 |
设Q到平面ABCD的距离为h,则
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
∴h=
| 1 |
| 3 |
又∵
| h |
| PA |
| BQ |
| BP |
| BQ |
| BP |
| 1 |
| 3 |
故PQ=
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
点评:本题主要考查面面垂直的性质定理,用余弦定理求解异面直线所成角和通过相似性来求解线段的长度等,培养学生转化化归的能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
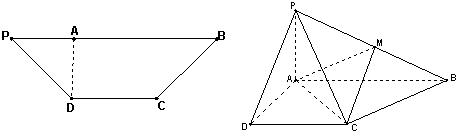
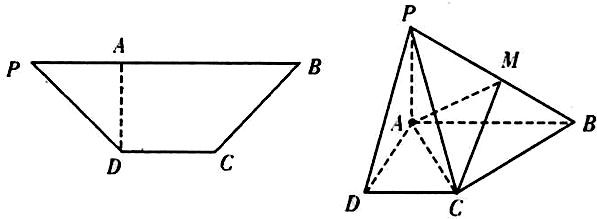
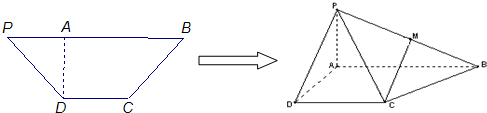
 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=