题目内容
已知f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,则f(3)的取值范围是( )
| A.[-1,20] | B.(-1,20) |
| C.[-7,26] | D.(-7,26) |
A
∵f(1)=a-c,f(2)=4a-c,
∴a= [f(2)-f(1)].
[f(2)-f(1)].
c=- f(1)+
f(1)+ f(2),
f(2),
∴f(3)=9a-c= f(2)-
f(2)- f(1).
f(1).
∵-1≤f(2)≤5,- ≤
≤ f(2)≤
f(2)≤ .
.
又-4≤f(1)≤-1, ≤-
≤- f(1)≤
f(1)≤ .
.
∴-1≤f(3)≤20.
∴a=
 [f(2)-f(1)].
[f(2)-f(1)].c=-
 f(1)+
f(1)+ f(2),
f(2),∴f(3)=9a-c=
 f(2)-
f(2)- f(1).
f(1).∵-1≤f(2)≤5,-
 ≤
≤ f(2)≤
f(2)≤ .
.又-4≤f(1)≤-1,
 ≤-
≤- f(1)≤
f(1)≤ .
.∴-1≤f(3)≤20.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
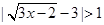 (2)
(2)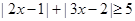
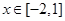 时,不等式
时,不等式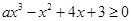 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )



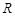 上定义运算
上定义运算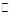 :
: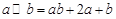 ,则满足
,则满足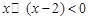 的实数
的实数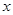 的取值范围为
的取值范围为




 a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( )
a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( ) ;
; ;
; -
- ,b=
,b= ,则以下结论正确的是( )
,则以下结论正确的是( ) ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )