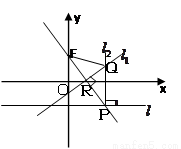题目内容
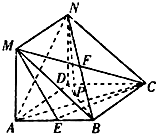如图，MA⊥平面ABCD，四边形ABCD是菱形，四边开ADNM是平行四边形．（Ⅰ）若E为AB的中点，求证：AN∥平面MEC；
（Ⅱ）若P为BD上的动点，求证：不论P在何位置，总有AC⊥NP．
分析：（1）通过证明四边形BCNM为平行四边形，证明F为BN的中点，根据EF是△ACM的中位线，证明EF∥AN，从而证明AN∥平面MEC；
（2）利用AM∥DN与AM⊥AC，证明DN⊥AC，再证明AC⊥BD，由线面垂直的判定定理可证明AC⊥平面BDN，从而证明AC垂直于平面内的所有直线．
（2）利用AM∥DN与AM⊥AC，证明DN⊥AC，再证明AC⊥BD，由线面垂直的判定定理可证明AC⊥平面BDN，从而证明AC垂直于平面内的所有直线．
解答：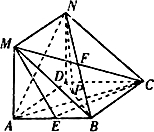
证明：（I）连接BN、CM，设BN∩CM=F，
∵四边形ABCD是菱形，四边形ADNM是平行四边形，
∴AD∥BC，AD∥MN，∴BC∥MN，
又AD=BC=MN，∴四边形BCNM为平行四边形，∴F为BN的中点，
∴EF∥AN，EF?平面MEC，AN?平面MEC，
∴AN∥平面MEC．
（II）∵MA⊥平面ABCD，AC?平面ABCD，∴AM⊥AC，
∵AM∥DN，∴DN⊥AC，
∵四边形ABCD是菱形，∴AC⊥BD，又∵BD∩DN=D
∴AC⊥平面BDN．
∵NP?平面BDN，∴AC⊥NP．
证明：（I）连接BN、CM，设BN∩CM=F，∵四边形ABCD是菱形，四边形ADNM是平行四边形，
∴AD∥BC，AD∥MN，∴BC∥MN，
又AD=BC=MN，∴四边形BCNM为平行四边形，∴F为BN的中点，
∴EF∥AN，EF?平面MEC，AN?平面MEC，
∴AN∥平面MEC．
（II）∵MA⊥平面ABCD，AC?平面ABCD，∴AM⊥AC，
∵AM∥DN，∴DN⊥AC，
∵四边形ABCD是菱形，∴AC⊥BD，又∵BD∩DN=D
∴AC⊥平面BDN．
∵NP?平面BDN，∴AC⊥NP．
点评：本题考查了线面平行的判定，考查了线面垂直的判定与性质，考查了学生的空间想象能力，推理论证努力．
练习册系列答案
名校课堂系列答案
相关题目
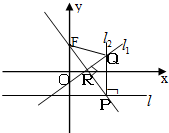（2012•威海二模）如图，在平面直角坐标系xoy中，设点F（0，p）（p＞0），直线l：y=-p，点p在直线l上移动，R是线段PF与x轴的交点，过R、P分别作直线l1、l2，使l1⊥PF，l2⊥l l1∩l2=Q．
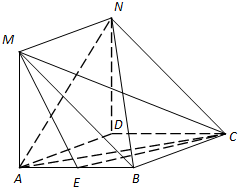（2013•武汉模拟）如图，MA⊥平面ABCD，四边形ABCD是菱形，且四边形ADNM是平行四边形．
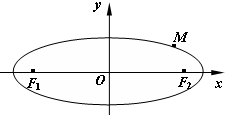（2013•盐城一模）如图，在平面直角坐标系xOy中，已知椭圆C：
、
，使
，
.