题目内容
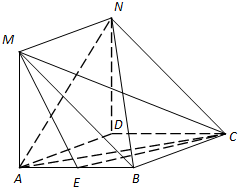（2013•武汉模拟）如图，MA⊥平面ABCD，四边形ABCD是菱形，且四边形ADNM是平行四边形．（Ⅰ）求证：AC⊥BN；
（Ⅱ）当点E在AB的什么位置时，使得AN∥平面MEC，并加以证明．
分析：（1）要证明AC⊥BN，只要证明AC⊥平面NDB，而由已知可知AC⊥BD，则只要证出AC⊥DN，结合已知容易证明
（2）当E为AB的中点时，设CM与BN交于F，由已知可得AN∥EF，结合线面平行的判定定理可证
（2）当E为AB的中点时，设CM与BN交于F，由已知可得AN∥EF，结合线面平行的判定定理可证
解答：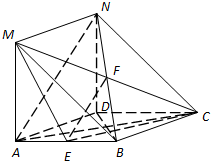
证明：（1）连接BD，则AC⊥BD．
由已知MA⊥平面ABCD，且四边形ADNM是平行四边形可得，DN⊥平面ABCD，
∴DN⊥AC
因为DN∩DB=D，
所以AC⊥平面NDB．
又因为BN?平面NDB，
所以AC⊥BN；
（2）当E为AB的中点时，有AN∥平面MEC．
CM与BN交于F，连接EF．
由已知可得四边形BCNM是平行四边形，F是BN的中点，
因为E是AB的中点，
所以AN∥EF．
又EF?平面MEC，AN?平面MEC，
所以AN∥平面MEC．
证明：（1）连接BD，则AC⊥BD．由已知MA⊥平面ABCD，且四边形ADNM是平行四边形可得，DN⊥平面ABCD，
∴DN⊥AC
因为DN∩DB=D，
所以AC⊥平面NDB．
又因为BN?平面NDB，
所以AC⊥BN；
（2）当E为AB的中点时，有AN∥平面MEC．
CM与BN交于F，连接EF．
由已知可得四边形BCNM是平行四边形，F是BN的中点，
因为E是AB的中点，
所以AN∥EF．
又EF?平面MEC，AN?平面MEC，
所以AN∥平面MEC．
点评：本题主要考查了线面垂直、线面平行的判定定理的简单应用，体现了线面、面面平行于垂直关系的相互转化．
练习册系列答案
相关题目