题目内容
7.不等式$\frac{6{x}^{2}-x-1}{{x}^{2}+1}$<0的解集为( )| A. | {x|x$>-\frac{1}{3}$} | B. | {x|x$<\frac{1}{2}$} | C. | {x|-$\frac{1}{3}<x<\frac{1}{2}$} | D. | {x|x$<-\frac{1}{3}$或x$>\frac{1}{2}$} |
分析 由x2+1≥1,得原不等式等价于6x2-x-1<0,由此能求出不等式$\frac{6{x}^{2}-x-1}{{x}^{2}+1}$<0的解集.
解答 解:∵x2+1≥1,$\frac{6{x}^{2}-x-1}{{x}^{2}+1}$<0,
∴6x2-x-1<0,
解方程6x2-x-1=0,得${x}_{1}=-\frac{1}{3}$,${x}_{2}=\frac{1}{2}$,
∴由6x2-x-1<0,得-$\frac{1}{3}<x<\frac{1}{2}$,
∴不等式$\frac{6{x}^{2}-x-1}{{x}^{2}+1}$<0的解集为{x|-$\frac{1}{3}<x<\frac{1}{2}$}.
故选:C.
点评 本题考查不等式的解集的求法,是基础题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.如图所示的程序框图,运行后输出结果为( )
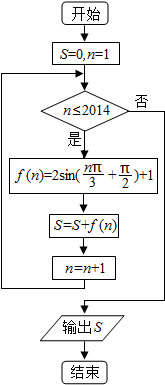

| A. | 2017 | B. | 4028 | C. | 2014 | D. | 2011 |
18.等差数列{an}中,a4=9,则前7项的和S7=( )
| A. | $\frac{63}{2}$ | B. | 28 | C. | 63 | D. | 36 |
12.已知|$\overrightarrow{OA}$|=$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则$\overrightarrow{OA}$•$\overrightarrow{AB}$等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
17.下列四个函数中,在(0,+∞)上单调递增的是( )
| A. | f(x)=1-2x | B. | f(x)=x2-3x | C. | f(x)=-$\frac{1}{x}$ | D. | f(x)=-|x| |