题目内容
【题目】不等式
－kx＋1≤0的解集非空，则k的取值范围为________．
【答案】(－∞，－
]∪[，＋∞)
【解析】由
－kx＋1≤0，得≤kx－1，设f(x)＝，g(x)＝kx－1，显然函数f(x)和g(x)的定义域都为[－2,2]．令y＝，两边平方得x2＋y2＝4，故函数f(x)的图象是以原点O为圆心，2为半径的圆在x轴上及其上方的部分．
而函数g(x)的图象是直线l：y＝kx－1在[－2,2]内的部分，该直线过点C(0，－1)，斜率为k.
如图，作出函数f(x)，g(x)的图象，不等式的解集非空，即直线l和半圆有公共点，可知k的几何意义就是半圆上的点与点C(0，－1)连线的斜率．
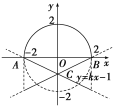
由图可知A(－2,0)，B(2,0)，故kAC＝
＝－，kBC＝
＝.
要使直线和半圆有公共点，则k≥或k≤－.
所以k的取值范围为(－∞，－]∪[，＋∞)．
练习册系列答案
相关题目
【题目】某工厂的甲、乙两个车间的
名工人进行了劳动技能大比拼，规定：技能成绩大于或等于
分为优秀， 
分以下为非优秀，统计成成绩后，得到如下的
列联表，且已知在甲、乙两个车间工人中随机抽取
人为优秀的概率为
.
优秀 | 非优秀 | 合计 | |
甲车间 |
| ||
乙车间 |
| ||
合计 |
|
（1）请完成上面的列联表；
（2）根据列联表的数据，若按
的可靠性要求，能否认为“成绩与车间有关系”？
