Question

已知△ABC中，∠C=90°，AC=3，BC=4．一个圆心为M，半径为的圆在△ABC内，沿着△ABC的边滚动一周回到原位．在滚动过程中，圆M至少与△ABC的一边相切，则点M到△ABC顶点的最短距离是________，点M的运动轨迹的周长是________．

Answer 1

    10
分析：由题意，当圆与AC，BC都相切时，M到C的距离最小；设点M的运动轨迹的周长为C，则点M的运动轨迹是一直角三角形，且与△ABC相似，由此可得结论．
解答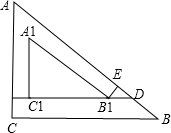：解：由题意，当圆与AC，BC都相切时，M到C的距离最小，因为圆的半径为，∠C=90°，所以MC=
设点M的运动轨迹的周长为C，则点M的运动轨迹是一直角三角形，且与△ABC相似，如图，
sin∠B=sin∠B₁DE=
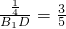
∴B₁D=，∴B₁C₁=4--=
∴，∴C=10
故答案为：，10．
点评：本题考查轨迹问题，考查学生分析解决问题的能力，属于中档题．