题目内容
已知△ABC中,∠C=90°,直线PA⊥平面ABC,若AB=5,AC=2,则点B到平面PAC的距离为( )
A、
| ||
B、
| ||
C、2
| ||
| D、5 |
分析:根据题目条件PA⊥BC,而BC⊥AC,PA∩AC=A,满足线面垂直的判定定理,故BC⊥面PAC,则点B到平面PAC的距离为BC,在Rt△ACB中,求出BC即可.
解答: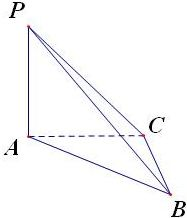 解:∵直线PA⊥平面ABC,BC?平面ABC
解:∵直线PA⊥平面ABC,BC?平面ABC
∴PA⊥BC,而BC⊥AC,PA∩AC=A
∴BC⊥面PAC,则点B到平面PAC的距离为BC
在Rt△ACB中,AC=2,AB=5则BC=
故选B
 解:∵直线PA⊥平面ABC,BC?平面ABC
解:∵直线PA⊥平面ABC,BC?平面ABC∴PA⊥BC,而BC⊥AC,PA∩AC=A
∴BC⊥面PAC,则点B到平面PAC的距离为BC
在Rt△ACB中,AC=2,AB=5则BC=
| 21 |
故选B
点评:本题主要考查了点、线、面间的距离计算,以及直线与平面垂直的性质,属于基础题.

练习册系列答案
相关题目
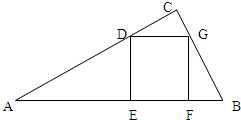 已知△ABC中,
已知△ABC中,