题目内容
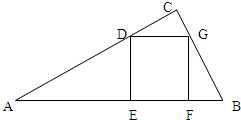 已知△ABC中,∠C=
已知△ABC中,∠C=| π |
| 2 |
设f(θ)=
| T |
| S |
分析:(1)首先在△ABC中利用边角关系得出:AC=a•tgθ.进一步得到用a,θ表示△ABC的面积S和正方形DEFG的面积即可;
(2)由(1)可得:f(θ)=
=
•
=
令u=
+
+1,sin2θ∈(0,1].利用基本不等式求得最大值即可,最后判断此时△ABC的形状.
(2)由(1)可得:f(θ)=
| T |
| S |
| a2sin2θ |
| (1+sinθcosθ)2 |
| 2 |
| a2tgθ |
| 2sinθ•cosθ |
| (1+sinθcos)2 |
| sin2θ |
| 4 |
| 1 |
| sin2θ |
解答:解:(1)∵在△ABC中,∴∠CBA=θ,BC=a.∴AC=a•tgθ.
∴S=
•a•atgθ=
tgθ,θ∈(0,
).…(2分) 设正方形DEFG边长为m,
则 CG=mcosθ,BG=
,∴BC=mcosθ+
=a. …(4分)
∴m=
,
∴T=m2=
,θ∈(0,
). …(6分)
(2)由(1)可得:f(θ)=
=
•
=
…(9分)
令u=
+
+1,sin2θ∈(0,1].
∵当
=
⇒sin2θ=±2∉(0,1],
∴当sin2θ=1时,u取得最小值,即f(θ)取得最大值.∴f(θ)=
的最大值为
.
此时sin2θ=1⇒θ=
.∴△ABC为等腰直角三角形. …(12分)
∴S=
| 1 |
| 2 |
| a2 |
| 2 |
| π |
| 2 |
则 CG=mcosθ,BG=
| m |
| sinθ |
| m |
| sinθ |
∴m=
| asinθ |
| 1+sinθ•cosθ |
∴T=m2=
| a2sin2θ |
| (1+sinθ•cosθ)2 |
| π |
| 2 |
(2)由(1)可得:f(θ)=
| T |
| S |
| a2sin2θ |
| (1+sinθcosθ)2 |
| 2 |
| a2tgθ |
| 2sinθ•cosθ |
| (1+sinθcos)2 |
…(9分)
|
令u=
| sin2θ |
| 4 |
| 1 |
| sin2θ |
∵当
| sin2θ |
| 4 |
| 1 |
| sin2θ |
∴当sin2θ=1时,u取得最小值,即f(θ)取得最大值.∴f(θ)=
| T |
| S |
| 4 |
| 9 |
此时sin2θ=1⇒θ=
| π |
| 4 |
点评:本小题主要考查在实际问题中建立三角函数模型、三角形的形状判断等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知△ABC中,∠C=90°,直线PA⊥平面ABC,若AB=5,AC=2,则点B到平面PAC的距离为( )
A、
| ||
B、
| ||
C、2
| ||
| D、5 |