题目内容
已知直线l1的方程为y=x,直线l2的方程为y=ax+b(a,b为实数),当直线l1与l2夹角的范围为[0, )时,a的取值范围是
)时,a的取值范围是
- A.(
 ,1)∪(1,
,1)∪(1, )
) - B.(0,1)
- C.(
 ,
, )
) - D.(1,
 )
)
A
分析:求出两条直线的斜率,利用两条直线的夹角公式,推出a的表达式,求出a的范围即可.
解答:直线l1的方程为y=x,斜率为:1;直线l2的方程为y=ax+b(a,b为实数),的斜率为:a;
因为tanθ=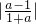 ,因为直线l1与l2夹角的范围为[0,
,因为直线l1与l2夹角的范围为[0, ),所以tanθ∈[0,2-
),所以tanθ∈[0,2- ),
),
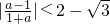 解得:a∈(
解得:a∈( ,1)∪(1,
,1)∪(1, )
)
故选A.
点评:本题是基础题,考查直线的夹角的求法,注意三角函数值的求解,绝对值不等式的解法,考查计算能力.
分析:求出两条直线的斜率,利用两条直线的夹角公式,推出a的表达式,求出a的范围即可.
解答:直线l1的方程为y=x,斜率为:1;直线l2的方程为y=ax+b(a,b为实数),的斜率为:a;
因为tanθ=
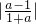 ,因为直线l1与l2夹角的范围为[0,
,因为直线l1与l2夹角的范围为[0, ),所以tanθ∈[0,2-
),所以tanθ∈[0,2- ),
),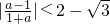 解得:a∈(
解得:a∈( ,1)∪(1,
,1)∪(1, )
)故选A.
点评:本题是基础题,考查直线的夹角的求法,注意三角函数值的求解,绝对值不等式的解法,考查计算能力.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知直线l1的方程为y=x,直线l2的方程为y=ax+b(a,b为实数),当直线l1与l2夹角的范围为[0,
)时,a的取值范围是( )
| π |
| 12 |
A、(
| ||||||
| B、(0,1) | ||||||
C、(
| ||||||
D、(1,
|