题目内容

【题目】设抛物线C的顶点在原点，焦点F在y轴上，开口向上，焦点到准线的距离为

(1)求抛物线的标准方程；

(2)已知抛物线C过焦点F的动直线l交抛物线于A、B两点，O为坐标原点，求证： 为定值．

【答案】(1) x2＝y.

(2)见解析

【解析】

(1)设出抛物线的方程，由焦点到准线的距离为可得，结合焦点在上，即可求得抛物线方程；(2)将直线方程代入抛物线方程，利用韦达定理及平面向量数量积的坐标运算，即可求得为定值.

(1)由焦点到准线的距离为知p＝，2p＝，抛物线的标准方程为x2＝y.

(2)设直线l的方程为：y＝kx＋，A(x1，y1)，B(x2，y2)．

由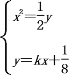

得：x2－kx－＝0，∴x1x2＝－

∴·＝x1x2＋y1y2＝x1x2＋4(x1x2)2＝－为定值

练习册系列答案
相关题目

【题目】已知，函数且.

（1）求p,q的值以及函数的表达式，并写出的定义域D；

（2）设函数，A=，集合，当时，求实数k的取值范围；

（3）当时，设，数列的前n项和为，直线的斜率为，是否存在实数，使对一切恒成立，若存在，分别求出实数的取值范围，若不存在，说明理由.

【题目】在直角坐标系xOy中，直线的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，直线与曲线C交于两点．

（1）求直线的普通方程和曲线C的直角坐标方程；

（2）求．

【题目】如图，已知四面体中，，且两两互相垂直，点是的中心．

（1）求二面角的大小（用反三角函数表示）；

（2）过作，垂足为，求绕直线旋转一周所形成的几何体的体积；

（3）将绕直线旋转一周，则在旋转过程中，直线与直线所成角记为，求的取值范围．

【题目】已知抛物线的焦点为F，F关于原点的对称点为P，过F作轴的垂线交抛物线于M，N两点，给出下列三个结论：

①必为直角三角形；

②直线必与抛物线相切；

③的面积为．其中正确的结论是___．

【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为 ，过点的直线的参数方程为（为参数），与交于两点

(1) 求的直角坐标方程和的普通方程；

(2) 若,,成等比数列，求的值.

【题目】下列说法错误的是（ ）

A. 若直线平面，直线平面，则直线不一定平行于直线

B. 若平面不垂直于平面，则内一定不存在直线垂直于平面

C. 若平面平面，则内一定不存在直线平行于平面

D. 若平面平面，平面平面，，则一定垂直于平面

【题目】已知椭圆：过点，且它的焦距是短轴长的倍.

（1）求椭圆的方程.

（2）若，是椭圆上的两个动点（，两点不关于轴对称），为坐标原点，，的斜率分别为，，问是否存在非零常数，使当时，的面积为定值？若存在，求的值；若不存在，请说明理由.

【题目】已知抛物线E：，圆C：．

若过抛物线E的焦点F的直线l与圆C相切，求直线l方程；

在的条件下，若直线l交抛物线E于A，B两点，x轴上是否存在点使为坐标原点？若存在，求出点M的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网