题目内容
(本题满分14分)
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F。
交PB于点F。
(I)证明  平面
平面 ;
;
(II)证明 平面EFD;
平面EFD;
(III)求二面角 的大小。
的大小。
【答案】
方法一:
(I)证明:连结AC,AC交BD于O。连结EO。
 底面ABCD是正方形,
底面ABCD是正方形, 点O是AC的中点
点O是AC的中点
在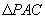 中,EO是中位线,
中,EO是中位线,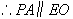 。
。
而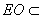 平面EDB且
平面EDB且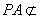 平面EDB,
平面EDB,
所以,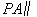 平面EDB。
平面EDB。
(II)证明: 底在ABCD且
底在ABCD且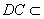 底面ABCD,
底面ABCD,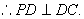
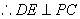 ① 同样由
① 同样由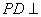 底面ABCD,得
底面ABCD,得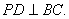
 底面ABCD是正方形,有
底面ABCD是正方形,有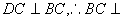 平面PDC
平面PDC
而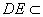 平面PDC,
平面PDC,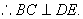 ② ………………………………6分
② ………………………………6分
由①和②推得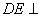 平面PBC 而
平面PBC 而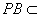 平面PBC,
平面PBC,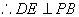
又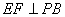 且
且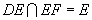 ,所以
,所以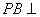 平面EFD
平面EFD
(III)解:由(II)知,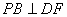 ,故
,故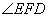 是二面角
是二面角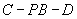 的平面角
的平面角
由(II)知,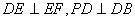 设正方形ABCD的边长为
设正方形ABCD的边长为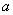 ,则
,则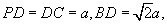
 在
在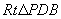 中,
中,
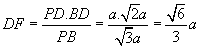 在
在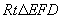 中,
中,
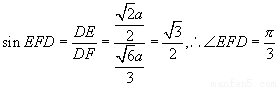 所以,二面角
所以,二面角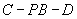 的大小为
的大小为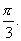
方法二:如图所示建立空间直角坐标系,D为坐标原点。设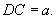
(I)证明:连结AC,AC交BD于G。连结EG。 依题意得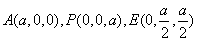
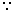 底面ABCD是正方形,
底面ABCD是正方形, 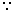
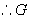 是此正方形的中心,
是此正方形的中心, 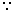 故点G的坐标为
故点G的坐标为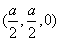 且
且
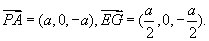
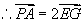 。这表明
。这表明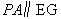 。
。
而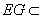 平面EDB且
平面EDB且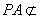 平面EDB,
平面EDB,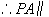 平面EDB。
平面EDB。
(II)证明:依题意得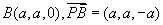 。又
。又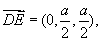 故
故
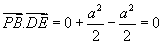
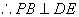
由已知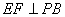 ,且
,且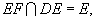 所以
所以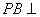 平面EFD。
平面EFD。
(III)解:设点F的坐标为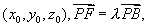 则
则
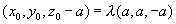
从而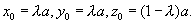 所以
所以
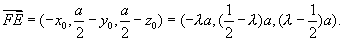
由条件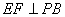 知,
知,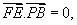 即
即
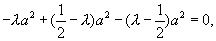 解得
解得 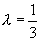 。
。
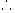 点F的坐标为
点F的坐标为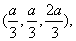 且
且

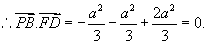
即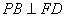 ,故
,故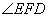 是二面角
是二面角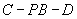 的平面角。
的平面角。
 且
且
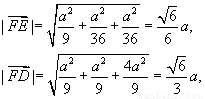
【解析】略

练习册系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).