Question

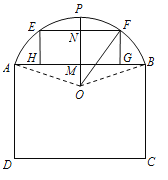
【题目】下图为某仓库一侧墙面的示意图，其下部是矩形ABCD，上部是圆弧AB，该圆弧所在的圆心为O，为了调节仓库内的湿度和温度，现要在墙面上开一个矩形的通风窗EFGH（其中E，F在圆弧AB上，G，H在弦AB上）.过O作，交AB 于M，交EF于N，交圆弧AB于P，已知（单位：m），记通风窗EFGH的面积为S（单位：）

（1）按下列要求建立函数关系式：

（i）设，将S表示成的函数；

（ii）设，将S表示成的函数；

（2）试问通风窗的高度MN为多少时，通风窗EFGH的面积S最大？

Answer 1

【答案】（1）详见解析；（2）4.5；

【解析】

试题（1）在Rt△OFN中用表示出NF和ON；用x表示出ON，再利用勾股定理求出NF；（2）用导数求函数的最值；

试题解析：（1）由题意知，OF＝OP＝10，MP＝6.5，故OM＝3.5．

（i）在Rt△ONF中，NF＝OFsinθ＝10sinθ，ON＝OFcosθ＝10cosθ．

在矩形EFGH中，EF＝2MF＝20sinθ，FG＝ON－OM＝10cosθ－3.5，

故S＝EF×FG＝20sinθ（10cosθ－3.5）＝10sinθ（20cosθ－7）．

即所求函数关系是S＝10sinθ（20cosθ－7），0＜θ＜θ0，其中cosθ0＝．

（ii）因为MN＝x，OM＝3.5，所以ON＝x＋3.5．

在Rt△ONF中，NF＝＝＝．

在矩形EFGH中，EF＝2NF＝，FG＝MN＝x，

故S＝EF×FG＝x．

即所求函数关系是S＝x，0＜x＜6.5．

（2）方法一：选择（i）中的函数模型：

令f（θ）＝sinθ（20cosθ－7），

则f ′（θ）＝cosθ（20cosθ－7）＋sinθ（－20sinθ）＝40cos2θ－7cosθ－20．

由f ′（θ）＝40cos2θ－7cosθ－20＝0，解得cosθ＝，或cosθ＝－．

因为0＜θ＜θ0，所以cosθ＞cosθ0，所以cosθ＝．

设cosα＝，且α为锐角，

则当θ∈（0，α）时，f ′（θ）＞0 ，f（θ）是增函数；当θ∈（α，θ0）时，f ′（θ）＜0 ，f（θ）是减函数，

所以当θ＝α，即cosθ＝时，f（θ）取到最大值，此时S有最大值．

即MN＝10cosθ－3.5＝4.5m时，通风窗的面积最大．

方法二：选择（ii）中的函数模型：

因为S＝，令f（x）＝x2（351－28x－4x2），

则f ′（x）＝－2x（2x－9）（4x＋39）．

因为当0＜x＜时 ，f ′（x）＞0，f（x）单调递增，当＜x＜时，f ′（x）＜0，f（x）单调递减，

所以当x＝时，f（x）取到最大值，此时S有最大值．

即MN＝x＝4.5m时，通风窗的面积最大．