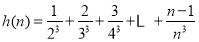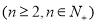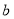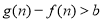题目内容
某班共30人，其中有15人喜爱篮球运动，有10人喜爱兵乓球运动，有3人对篮球和兵乓球两种运动都喜爱，则该班对篮球和乒乓球运动都不喜爱的人数有___________.
12
【解析】
试题分析：设两者都喜欢的人数为x人，则只喜爱篮球的有（15-x）人，只喜爱乒乓球的有（10-x）人，由此可得（15-x）+（10-x）+x+8=30，解得x=3，所以15-x=12，即所求人数为12人，故答案为：12．
考点：交、并、补集的混合运算.
练习册系列答案
能力评价系列答案
相关题目
某地最近十年粮食需求量逐年上升，下表是部分统计数据：
年份 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
需求量（万吨） | 3 | 6 | 5 | 7 | 8 |
（1）利用所给数据求年需求量与年份之间的回归直线方程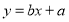
；
（2）利用（1）中所求出的直线方程预测该地第6年的粮食需求量．
