题目内容
求证:关于x的方程x2+2ax+b="0" 有实数根,且两根均小于2的充分但不必要条件是a≥2且|b| ≤4.
同解析。
先证充分性,而必要性只需要通过举反例来否定.
先证明条件的充分性:
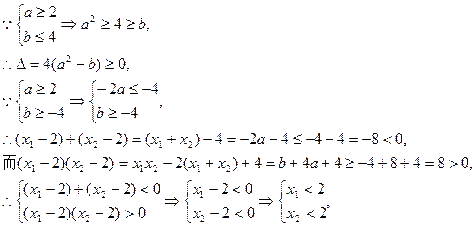 ①、②知“a≥2且|b|≤4”
①、②知“a≥2且|b|≤4”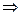 “方程有实数根,且两根均小于2”.
“方程有实数根,且两根均小于2”.
再验证条件不必要:
∵方程x2-x=0的两根为x1="0," x2=1,则方程的两根均小于2,而a=-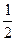 <2,
<2,
∴“方程的两根小于2”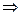 “a≥2且|b|≤4”.
“a≥2且|b|≤4”.
综上,a≥2且|b|≤4是方程有实数根且两根均小于2的充分但不必要条件
先证明条件的充分性:
|
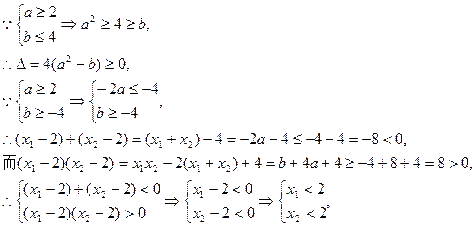 ①、②知“a≥2且|b|≤4”
①、②知“a≥2且|b|≤4”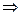 “方程有实数根,且两根均小于2”.
“方程有实数根,且两根均小于2”.再验证条件不必要:
∵方程x2-x=0的两根为x1="0," x2=1,则方程的两根均小于2,而a=-
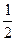 <2,
<2,∴“方程的两根小于2”
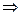 “a≥2且|b|≤4”.
“a≥2且|b|≤4”.综上,a≥2且|b|≤4是方程有实数根且两根均小于2的充分但不必要条件

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
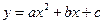 的图象与
的图象与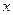 轴交于
轴交于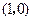 的充要条件为
的充要条件为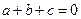 .
.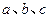 是常数,则“
是常数,则“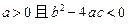 ”是“对任意
”是“对任意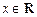 ,有
,有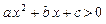 ”的 ( )
”的 ( ) 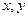 中至少有一个小于0”是“
中至少有一个小于0”是“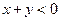 ”的( )
”的( )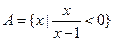 ,
,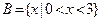 ,那么“
,那么“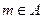 ”是“
”是“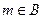 ”的( )
”的( )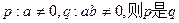 的 ( )
的 ( )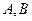 为
为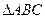 的两内角,则“
的两内角,则“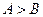 ”是“
”是“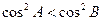 ”的如下哪个条件( )
”的如下哪个条件( )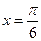 ”是“
”是“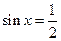 ”的充分不必要条件;
”的充分不必要条件;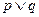 ”为真,则“
”为真,则“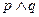 ”为真;
”为真;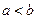 ,则
,则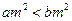 ;
;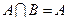 ,则
,则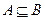 。
。 ,q:
,q: 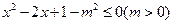 ,若
,若 是
是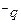 的必要不充分条件,求实数m的取值范围.
的必要不充分条件,求实数m的取值范围.