题目内容
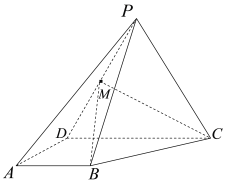
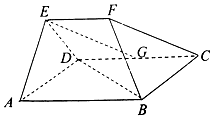
【题目】如图,几何体![]() 中,
中,![]() 为边长为2的正方形,
为边长为2的正方形,![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
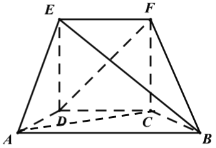
(1)求证:![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)证明:由题意得![]() ,
,![]()
![]()
![]() 平面
平面![]()
![]()
![]() ,
,
又![]()
![]()
![]() 平面
平面![]()
![]()
![]() ,再由勾股定理得
,再由勾股定理得![]()
![]()
![]()
![]()
![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系,平面
轴建立如图所示的空间直角坐标系,平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量为
的法向量为![]()
![]()
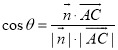
![]()
![]()
![]()
![]() .
.
试题解析: (1)证明:由题意得,![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵四边形![]() 为正方形,∴
为正方形,∴![]() ,
,
由![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,则有
,则有![]() ,∴
,∴![]() ,
,
由![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() 所在的直线相互垂直,故以
所在的直线相互垂直,故以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由(1)知平面![]() 的法向量为
的法向量为![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则有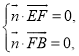 即
即![]() 即
即![]()
令![]() ,则
,则![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,
,
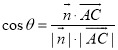
![]()
![]() ,
,
∵![]() ,∴
,∴![]() .
.

【题目】某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了20位家长的满意度评分,其频数分布表如下:
满意度评分分组 |
|
|
|
|
| 合计 |
高一 | 1 | 3 | 6 | 6 | 4 | 20 |
高二 | 2 | 6 | 5 | 5 | 2 | 20 |
根据评分,将家长的满意度从低到高分为三个等级:
满意度评分 | 评分 | 70 | 评分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取1名家长,记事件![]() :“高一家长的满意度等级高于高二家长的满意度等级”,则事件
:“高一家长的满意度等级高于高二家长的满意度等级”,则事件![]() 发生的概率为__________.
发生的概率为__________.
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
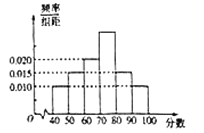
(1)求得分在![]() 上的频率;
上的频率;
(2)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(3)由于部分居民认为此项学习不具有必要性,![]() 社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
认为此项学习十分必要 | 认为此项学习不必要 | |
50岁以上 | 400 | 600 |
50岁及50岁以下 | 800 | 200 |
根据上述数据,计算是否有![]() 的把握认为居民的学习态度与年龄相关.
的把握认为居民的学习态度与年龄相关.
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |