Question

已知椭圆的右焦点为，点在椭圆上，以点为圆心的圆与轴相切，且同时与轴相切于椭圆的右焦点，则椭圆的离心率为         ．

 

Answer 1

【答案】

【解析】

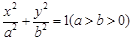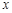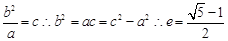试题分析：根据题意可知，椭圆的右焦点为，点在椭圆上，由于以点为圆心的圆与轴相切，可知圆心的横坐标即为圆的半径，且同时与轴相切于椭圆的右焦点，则说明了PF垂直于x轴，且利用椭圆的通径长为则说明半径r=,那么点P的横坐标为C,故可知，因此答案为

考点：本试题考查了椭圆的性质运用。

点评：解决该试题的关键是能结合题目中圆于两坐标轴相切，则说明了点P的坐标，然后利用半径一样来得到a,b,c的关系式，进而求解s椭圆的离心率，属于中档题。